Ai Plan (04) PDDL

Ai Plan (04) PDDL

Yimi
by Yimi

Categories

Tags

Table of Contents

  1. PDDL (Planning domain definition language ,规划域定义语言)
  2. 对象类型的定义
  3. 关系的表示
  4. 状态的表示
  5. 操作（Operator）的表示
  6. 从状态中找出合适的行动

literals ：字面量，由语法表达式定义的常量，或由一组定义好的字词组成点语句表达式定义的常量

PDDL (Planning domain definition language ,规划域定义语言)

是一种尝试用来规范 AI规划 的语言 ，与1998年开发。是一种一阶语言（first-order language） L 语言，其定义了我们如何使用有限的单词和符号来形成复杂的，类似句子的实体。它把规划问题的模型分为两个主要部分：领域描述（domain description） 和 问题描述（problem description）

领域描述

  • 域名定义
  • 需求定义
  • 对象类型层次结构定义（与OOP中的类层次结构类似）
  • 常量对象点定义
  • 谓词的定义
  • 可能采取的动作（action）的定义
    • 带有参数的Operator方案，会在执行过程中实例化
    • 动作具有参数(可以是对象实例化的变量)，前提条件和效果。效果也可以具有应用条件

问题的描述

  • 问题名称的定义
  • 相关域名的定义
  • 所有可能对象的定义
  • 初始条件的定义
  • 目标状态的定义

PDDL语法：

  • 首个单词是谓词，用来修饰后面的对象的关系
  • 变量以?开头
  • -之后跟随的是变量的类型
  • ;后的是注释说明
  • 每条关系的声明中的变量都是互不干扰的，都是局部变量，仅在本条声明中有效

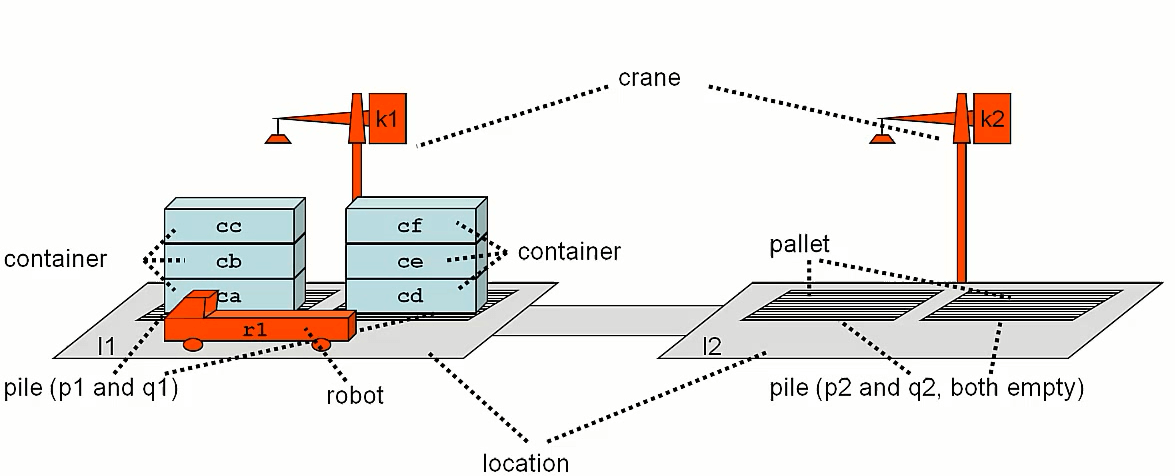
本文使用的例子是码头工作机器人(dock-worker-robot)，后面简称为 DWR 的例子 image-center

对象类型的定义

在DWR点定义域中，我们拥有以下几种类型的对象 我们使用不同的字符来标记这些对象，如robot1,robot2， 分析场景中的对象

  • robots {robot1,robot2,… }
    • 集装箱搬运者
    • 可以在邻近的两个地点间移动
  • crane {crane1,crane2,… }
    • 起重机，只能固定在某个地点
    • 可以吊起搬运者或桩子上的集装箱
    • 可以把集装箱放在搬运者或桩子上
  • containers {cont1,cont2,… }
    • 集装箱，放置在桩子上
    • 可以被搬运者搬运
    • 可以被起重机吊起
  • locations {loc1,loc2,… }
    • 表示地点位置
  • piles {p1,p2,… }
    • 桩子，属于某个地点
    • 可以放置托盘
  • pallet
    • 可以承载集装箱

然后我们可以用PDDL表示这些类型

(define(domain DWR)               ;告诉系统开始定义,定义的东西是 domain,名称为DWR
  (:requirement :strips :typing)  ;此特定领域的需要strips和typing这两个扩展
  (:types
    location                      ;可以拥有多个不同的地点
    pile                          ;附属在地点之上的桩子
    robot                         ;最多可以装载一个集装箱,每个地点只能有一个搬运者
    crane                         ;属于某个地点,用来吊起和放下集装箱
    container                     ;集装箱
  )
  ...
)

关系的表示

我们使用谓语动词来联系两个对象，因此，我们需要定义一些关系用来联系对象彼此。关系也被称为给定世界中的谓词（predicates），用来陈述几个对象间的关系是持有还是不持有，是正还是假。

(:predicates
  ;前三条什么是静态的，即不会改变他们的关系
  (adjacent ?l1 ?l2 - location)       ;location ?l1 is adjacent to ?l2
  (attached ?p - pile ?l - location)  ;pile ?p is attached to location ?l
  (belong ?k - crane ?l - location)   ;crane ?k belongs to location ?l

  ;下面四条是关系动态的
  (at ?r - robot ?l - location)       ;robot ?r is at location ?l
  (occupied ?l - location)            ;there is a robot at location ?l
  (loaded ?r - robot ?c - container)  ;robot ?r is loaded with container >c
  (unloaded ?r - robot)               ;robot ?r is empty

  ;这两个关系是相互关联的，即起重机为空时，它就不是握着集装箱；反之亦然，如果它握着集装箱，则它不可能为空
  (holding ?k - crane ?c - container)  ;crane ?k is holding a container ?c
  (empty ?k - crane)                  ;crane ?k is empty

  (in ?c - container ?p - pile)       ;container ?c is within pile ?p
  (top ?c - container ?p - pile)      ;container ?c is on the top of pile ?p
  (on ?c1 - container ?c2 - container);container ?c1 is on container ?c2
)

状态的表示

原子：一个谓语加上适当数量的对象构成一个原子 状态：是一组原子(atom)集合的实例对象（即具备实际意义，某个时刻，世界中对象间的关系）

  • 是一个封闭世界，只有在状态的声明中提到的关系才成立，其他的一律不成立

如图，可以把该状态描述如下:

state = {
  adjacent(loc1,loc2),adjacent(loc2,loc1),
  attached(p1,loc1),attached(p2,loc1),
  belong(crane1,loc1),
  at(r1,loc2),
  occupied(loc2),
  empty(crane1),
  in(c1,p1),in(c3,p1),
  on(c3,c1),on(c1,pallet),
  top(c3,p1),
  in(c2,p2),
  on(c2,pallet),
  top(c2,p2)
}

at(r1,loc1)是正确的吗？ ——答案是，错误的，因为不在state的描述当中。 以上就是state的表示

操作（Operator）的表示

操作提供状态过渡的状态高度系统，在规划定义域中，它由一个三元组组成，即

o = (name(o), precond(o),effects(o))

  • 表示此操作的唯一名称，不能和其他名称重命名，并且包含一系列参数，在执行操作时需要用到的变量
  • precond(o) 表示 前提条件
  • effects(o) 表示 作用效果
  • precon(o) 和 effects(o) 都是一组字面量集合

行为则是一个定义域中的某个操作的实例，当然，在规划时可以有许多同一个操作的行为同时存在。

move(r,l,main)

  • precond:adjacent(l,m),at(r,l),¬occupied(m)
  • effects: at(r,m),occupied(m),¬occupied(l),¬at(r,l)

load(k,l,c,r)

  • precond: belong(k,l),holding(k,c),at(r,l),unloaded(r)
  • effects: empty(k),¬holding(k,c),loaded(r,c),¬unloaded(r)

put(k,l,c,d,p)

  • precond:belong(k,l),attached(p,l),holding(k,c),top(d,p)
  • effects: ¬holding(k,c),empty(k),in(c,p),top(c,p),on(c,d),¬top(d,p)
;; move a robot between two adjacent locations
(:action move
  :parameters (?r - robot ?from ?to - location)
  :precondition(and
    (adjacent ?from ?to) (at ?r ?from) (not(occupied ?to))
    )
  :effect(and
    (at ?r ?to) (occupied ?to) (not(occupied ?from)) (not(at ?r ?from))
    )
)

从状态中找出合适的行动

假设 L 是一组字面量集合

  • L+ 表示L中的所有正向字面量
  • L- 表示L中的所有反向字面量

假设a是一个行为，s是一个状态，当且仅当a在s中可用时

  • precon+(a) ⊆ s
  • precon-(a) ∩ s = {} ;例如a 中有一个条件为 ¬occupied(m),m没有被占用，与s点交集一定为空，即s中一定没有occupied(m)这条记录。

注意：s所维护的关系记录是通过添加和删除表示的，也就是说，当s中存在某条描述时，条件为真，不存在某条描述时，条件为假。当我们通过反向字面量进行操作时，其实就是移除掉这一项，如 对occupied(m)，执行效果¬occupied(m)，就是将m被占用，改为m没有被占用，就没必要在新的状态中特定记录没有被占用这么一条记录，只要该状态没有该记录，就表示occupied(m)这条语句的结果为假

最后，我们把s状态中的行为a 的状态转移函数γ 定义如下

  • γ(s,a) = (s - effects-(a)) ∪ effects+(a)

即，新的状态 = s 移除掉a的效果中的所有反向记录 ∪ a的效果中的所有正向记录

某个状态可能有许多行动，我们需要从中找出合适的行动 那么如何找出合适的行动呢？

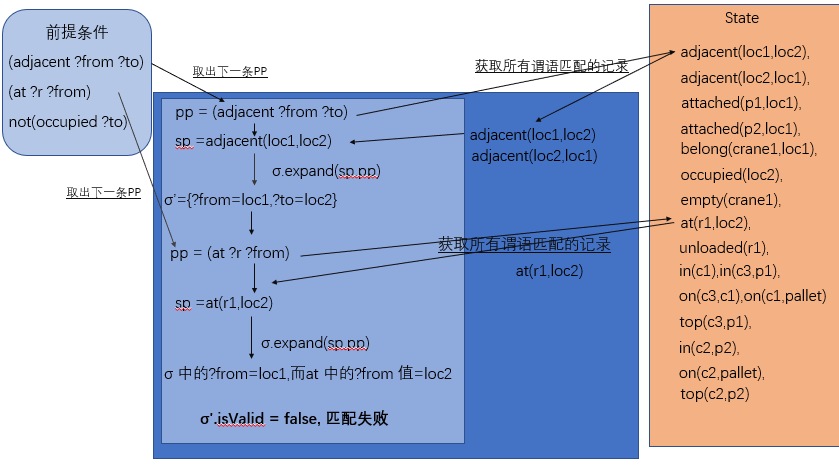
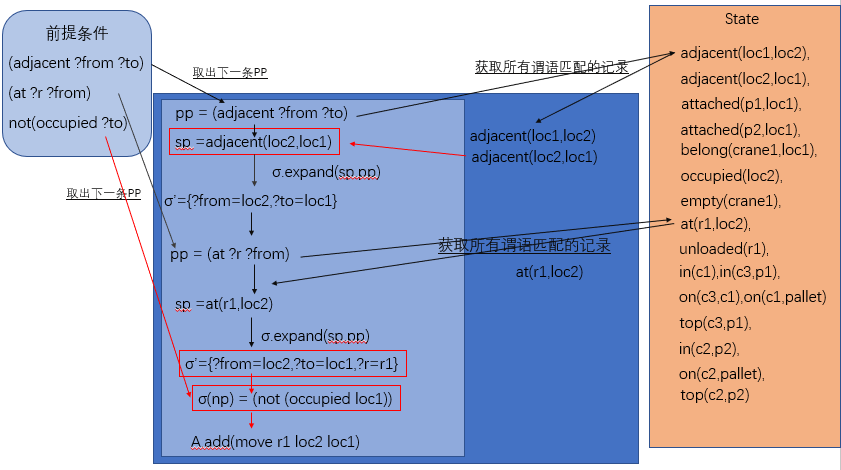
function addApplicables(A,op ,precs, σ,s)
  if precs+.isEmpty() then
    for every np in precs- do
      if s.falsifies(σ(np)) then return
    A.add(σ(op))
  else
    pp← precs+.chooseOne()
    for every sp in s do
      σ' ← σ.extend(sp,pp)
      if σ'.isValid() then
        addApplicables(A,op,(precs - pp),σ',s)

解析该算法：

  • 参数
    • A是我们最终返回的可用行动集合，最初是空的
    • op 是 operator，当前状态合适的操作点实例
    • precs 是preconditions，该operator点前提条件
    • σ 是操作所需变量的值的集合，初始时没有变量，每次匹配条件成功时增加记录
    • s 当前的状态

首先处理所有的正字面量条件，所以，先用precs+.isEmpty()检测是否有正字面量的前提条件，有的话，执行else中的部分

  • 首先获取下一个正字面量pp(positive precondtion)
  • 遍历所有的state中的声明sp（state propositions），同时他会过滤掉其他记录，只留下谓词相同的
    • 生成新的σ’ = σ.extend(sp,pp)，里面存放的是前提条件的pp，和状态中的sp
    • 判断σ’.isValid ,sp 是否满足 pp，谓词相同，变量相同
      • 是，将pp 从precs中去掉，σ’ 作为新的 σ，继续判断剩余的条件，，直到precs为空，然后把a添加到可行行为列表中
  • 另外，就是，当前提条件的正字面量为空后，开始判断所有负字面量
    • 遍历precs-中的每一个 np （negative precondition）
      • 检测s是否包含np这个记录，如果有，则判断失败。因为，不允许s中拥有任何负字面量的定义。（如负字面量¬occupied(m) 表示m不被占用,而s中有occupied(m)，m被占用这一条记录，显然不符合条件）
    • 前面的负字面量全部通过，说明该操作是合适的，因此把op加入A列表中。
  • σ(np) 解释，给np这条记录赋值，使其有真正意义的值，然后与s中的记录进行对比
  • σ(op) 解释，把σ中所有记录应用给op的参数，使其成为实例

实例： 假设当前的世界状态为 image-center 需要判断的行动为move image-center 然后就是该行动是否可用的判断过程 image-center image-center

LinkedIn Reddit