Table of Contents
经典规划
- 任务：找出规划问题的解决方案
- 规划问题由3部分组成
- 初始状态
- 由一组命题组成（描述有哪些对象，这些对象之间的关系，这些对象的属性）
- 规划定义域 (plannig domain)
- 实质上由一系列的operators组成(某个操作包含name , preconditions , effects)
- 定义域其实上一个可重用的组件，不同的问题可能都需要类似的操作，只不过是初始状态和最终目标有所不同
- 目标状态
- 初始状态
- 解决方案（plan）
规划域 Planning Domain
对于定义域 ∑ = (S,A,γ) 是一个受限的状态转移系统
- S为所有状态的集合，是一组落地的原子对象（即运行中的实例）
- A为规划操作(planning operators) O 的一些实例的集合
- γ 为过渡函数，其定义了所有状态的过渡映射
- 即，s’ = γ(s,a), 在s状态，应用动作a，可以得到状态s’
- S x A -> S ,
- 当a对于s可用时， γ(s,a) = s( s - effects-(a)) ∪ effects+(a)
- 如果a对于s不可以，则 γ(s,a) = s’ 未定义 ,即s’ 不在S中
- S 对于 γ 是封闭的，即不存在通过γ获取的状态不属于S
下面是之前的DWR 定义域 的 PDDL 完整版
规划问题 Planning Problems
P = (∑,si,g)
- ∑ 是前面提到的规划定义域
- 初始状态:si ， si ∈ S
- g 是一组描述最终目标的 字面量
- 因此， 一个目标状态的集合应该符合
S<sub>g</sub> = {s ∈ S | s 满足 g }
- 因此， 一个目标状态的集合应该符合
所以，Planning Problems 的实质是一个具体的问题，即在某个规划领域中，从某个初始状态到达某个目标状态的求解。
下面是DWR Problem 的 PDDL 代码
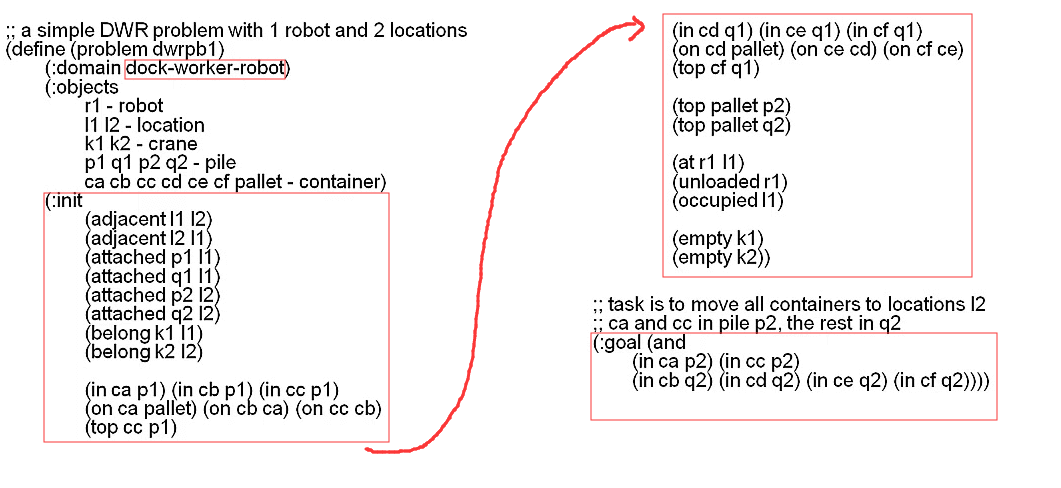我们在里面定义了问题名称，使用哪些对象，初始状态，目标状态，使用那一个定义域
典型计划 Classic Plans
计划是有一系列的行动 π = <a1,…,ak> (k >= 0) 组成
- 计划π的长度
|π|= k，即行动的数量 - 如果 π1 = <a1,…,ak> , π2 = <b1,…,bj>，则它们可以连接为新的计划 π1·π2 = <a1,…,ak,b1,…,bj>
- 把状态转换扩展到计划层面
- 如果k = 0,即计划为空，则 γ(s,π) = s
- 如果k > 0且a1对于s可用 ，则 γ(s,π) = γ( γ(s,a1),<a2,ak>)
- 递归执行完π中的所有行为
- 其他情况，γ(s,π)未定义
假设有一个规划问题P = (∑,si,g)，当γ(si,π)的结果满足g时，计划 π 是 P 的一个解决方案！
- 当 π的某个合适的子序列也是p的解决方案时，π是冗余的
- 当不存在其他解决方案的行动个数比π小，那么π是最小的