Table of Contents
与前向搜索相反，前向搜索从初始状态开始，在状态空间进行搜索直到找到最终目标；后向搜索则是从最终目标开始在状态空间进行反向搜索，直到找到初始目标！它非常简单，且和前向搜索也非常相似。
相关性（Relevance）和回归集（Regression Set）
我们从两个定义开始，相关性（Relevance）和回归集（Regression Set） 假设有一个规划问题，P = (∑,si,g)，里面的三个前面已经见过多次了，分别是状态转换系统，初始状态，目标状态。 相关性 ：当a ∈ A 是 和g的相关时
- g ∩ effects(a) != {} ,表示行动必须对目标有影响
- g+ ∩ effects-(a) = {} 且 g- ∩ effects+(a) = {} ，表示行动的效果不能与目标有所冲突
回归集 ：g 和 相关的行为a 的回归集 γ-1(g,a) = (g - effects(a)) ∪ precond(a)
- 正如你看到的，γ-1(g,a) ,和前面的状态转移函数 ∑ = γ(s,a) 相反，即它是状态转移函数的逆函数。
- 它的计算是，移除掉所有行动的效果，加上该行动的前提条件，来得到一个新的目标，对比该新目标和初始状态是否相等，如果相等证明搜索成功；否则，进行后向搜索，直到找到初始状态。
回归函数
和前向搜索的分析类似,则对于定义域∑ = (S,A,γ), Γ-m 表示 m 步时后向搜索的状态集，当该状态机中包含初始状态时，表明搜索成功，且说明至少需要m步才能回溯到初始状态。
- Γ-1(g) = { γ-1(g,a)
|a ∈ A 且 a 与 g 相关 } - 对于多个目标 g1,…,gn ,都是回溯后的子目标,假设我们处于某一个子目标，当我们想要定义我们可以回溯到哪些节点，即有哪些前继节点时
- Γ-1( {g1,…,gn} ) = ∪k∈[1,n]Γ-1(gk)
- 计算出每一个状态的Γ-1(g),然后将他们合并，得到一个结果集。无论输入那些子目标中的任意一个，都可以一步取得所有可达前继节点。
- 为使得这个定义更加通用一些，通过定义我们规定的步数，来限定结果集。意义是，某一组目标，通过m步，可以抵达另一组目标。
- Γ-0( {g1,…,gn} ) = {g1,…,gn}
- 当步数为0时，我们哪也去不了，只能留在原地
- Γ-m( {g1,…,gn} ) =Γ-1 ( Γ-(m-1)( {g1,…,gn}))
- 当步数为m时，通过递归这些结果集得到最终结果集的合并。
- Γ-0( {g1,…,gn} ) = {g1,…,gn}
- Γ-1( {g1,…,gn} ) = ∪k∈[1,n]Γ-1(gk)
类似的，过渡闭路则定义:从最终目标开始，可以回溯的所有状态
Γ﹤(s)=∪(k∈[1,∞])Γ-k({s})=Γ-0(g)∪Γ-1(g) ∪Γ-2(g)∪…∪Γ-k(g)
最后，把状态空间规划作为搜索问题 已知 规划问题 P = (O,si,g)，作为搜索问题
- 初始状态 = g
- 最终目标的满足检测: 如果当前s 满足 si时，说明找到起始状态si
- 路径成本函数:
π = |π|，等于路径的长度 - 状态s前继节点函数 : Γ-1(s)
优点与缺点
后向搜索同样也可能会有非常巨大的分支！当与g相关的操作o可能有许多实例,a1,a2,…,ai
像unstack行动，操作集O中有许多unstack的实例，他们只是输入参数的值不一样
unstack(b1,b1),unstack(b1,b2),..， 而a1,…,ai的中的大部分的前提条件可能都无法从初始状态到达，和之前一样，对这样的节点进行深入的搜索会浪费大量的时间！
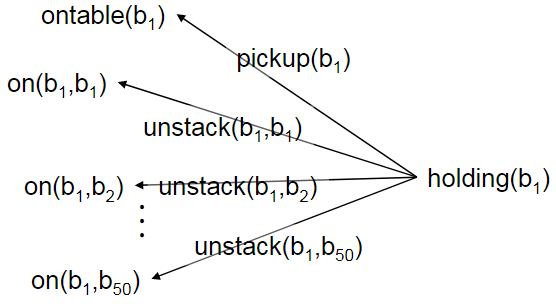我们可用通过把这些形式相同，只是传入参数不同的合并为一个，即简单的把这些不同输入的部分以变量的形式保存，即变成下面这种形式：
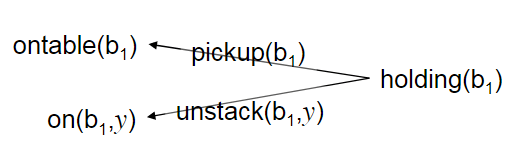
这种方法称为抬升(Lifting)
- 比后向搜索更加复杂，必须跟踪执行了哪些替代操作
- 但是分支比后向搜索小得多
这里先不深入讨论，后面有一篇会专门讨论局部规划，就是使用了这种方法！
搜索空间还是很大！ 尽管抬升后向搜索(lifted-backward-search)生成了比简单的后向搜索更加小的搜索空间，但是它还是有点大。
- 假设行动a,b,c是独立的，行动d必须在它们之前执行，且没有从s0到d的输入状态的路径
- 在意识到没有解决方案前，我们将尝试a,b,c的所有可能排序
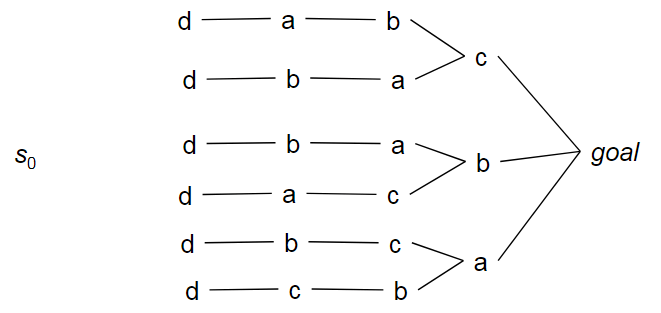这里先不深入讨论，后面会有一篇文章 计划空间规划 来专门讨论！