Ai Plan (08) 局部规划

State-Space vs. Plan-Space
plan-space sarch
计划空间规划-基本思想
总结：

State-Space vs. Plan-Space

在前面的文章中，我们所使用搜索空间都是状态空间，即state-space

节点，表示世界中的某个状态
路径，表示该空间下的一个计划

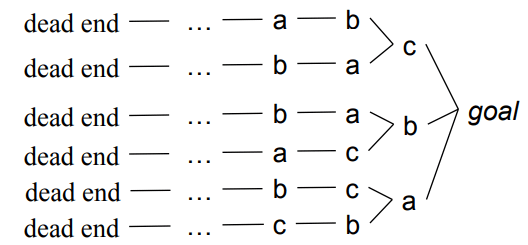
前面说过，状态空间存在一些问题，当有同一组行动会找不到结果时，在意识到这个问题之前，我们的算法已经把这一组行动的所有排列组合尝试过了，这会导致很多不必要的搜索。 image-center

这一次，我们来聊聊计划空间 plan-space 以及局部计划，它使用了一种新的规划策略，最少递交策略，不提交顺序，实例等，除非真的需要才会对其展开。

plan-space sarch

对比状态空间，计划空间也会有节点，弧，路径这些概念，只不过其含义不太一样

节点：该图中的节点都是些局部计划，不是完整可执行的计划
弧：计划完善操作，它们告诉我们如何在这些节点间转移。通常是通过细化它们(添加更多的内容到这些计划上)
- 这里所说的内容有四种
  - 新的行动
  - 新的约束
    - 顺序约束
    - 变量绑定约束
    - 因果关系约束（因果关系约束隐式包含了顺序约束）
路径：即解决方案，它是一个偏序计划（partial-order plans）
- 偏序是指，任意a,b ∈ S,它们之间的关系要么是a < b,要么是a >b ,要么是a = b，要么不可比较，即该集合中的元素的排序顺序是不确定的
- 假设规划问题p = (∑,s_i,g) ，只有偏序计划 π = (A,‹，B,L) 满足以下条件时，它才是问题的解决方案
  - 满足排序约束‹ ，且无循环
  - 所有变量与B中的绑定变量一致，可以在B中找到所有变量的值，以及满足各种约束（= 、≠）
  - 对于A中所有行动的序列< a₁,… a_k >
    - 该序列是全序的，全部实例化的，且遵循排序约束‹ 和变量绑定约束 B
    - γ(s_i , < a₁,… a_k >) 得到的最终结果满足 g

计划空间规划-基本思想

从最终目标开始进行后向搜索
搜索空间中的每个节点都是一个局部计划
- 一组部分实例化的行动
- 一组约束
对该节点不断细化直到得到一个完整的解决方案
约束的类型
- 优先级约束，形如(a ‹ b ),即a优先于b
- 绑定约束
  - 不相等约束，如 v1 ≠ v2 或 v≠ c （v 表示变量， c 表示常量）
  - 相等约束，如 v1 = v2或v=c
- 因果关系链，形如 < a-[p]→ b >
  - 行动b 需要前提 p, 行动a可以用来实现该前提

image-center

计划空间中的节点-局部计划(Partial Plans)

接下来，什么是局部计划，局部计划的定义是什么？我们知道，计划（Plan），是组织成某种结构的一组行动，这种结构通常是一个序列。那么，局部计划是计划的部分(不完整)实现

这些行动的子集
这些组织结构的子集，降级为原结构中的某些属性得到的子集，如
- 行动的时间顺序
- 基本联系，即行动的前因后果（前提条件，作用效果）
变量绑定的子集(一组行动所需的变量所绑定的实例值的集合)

以上意味着我们有四种方式来创建局部计划，即仅包括动作的子集，时序的子集，基本联系的子集，变量的子集。

局部计划的定义 局部计划是一个四元组，记为 π = (A,‹,B,L)，其中

A = {a₁,…,a_k} 是一组规划操作的部分实例
‹ 是一组 A 中的行动的顺序约束，形如(a_i ‹ a_j)，即a_i 必须先于 a_j
B 是一组 A 中的行动的变量约束
- 这些变量绑定告诉我们这些变量可以取什么值
- 比起分配特别值给变量，变量绑定约束可以更加笼统，我们可以使用下面三种形式
  - x = y，两个变量必须有相同的值
  - x ≠ y，两个变量必须有不同的值
  - x ∈ D_x（给定一个变量域，x的值需要属于给定的一组值当中）
L 是一组行动间的因果关系，形如< a_i - [p] -> a_j >
- a_i,a_j 是 A 中的行动
- 顺序满足约束(a_i ‹ a_j)，即a_i 先于 a_j
- 命题p 是 a_i 的作用效果，是a_j的前提条件
- 变量a_i,a_j中出现在命题p中的变量的绑定约束，需要定义在B中

计划空间中的过渡-细化操作(Refinemnt Operations)

计划空间中的节点转移可以理解为计划细化操作，它们将一个局部计划细化为另一个局部计划，因为局部计划由四个部分组成，细化操作也由四个部分组成。

1.添加行动，以行动的初始状态，目标条件，不同变量的操作集来表示局部计划的简化了其表示形式

什么时候会添加一个新的行动到局部计划中
- 有未满足的前提条件
- 有未满足的目标条件

2.添加因果关系链，从生产者连接到消费者

生产者可以是行动的效果或者初始状态；消费者可以是行动的前提或者最终目标的前提
目的：为了防止其他行动的影响，以及追踪已经实现的前提条件

3.添加变量绑定

每次为添加新的操作实例时，都会引入该操作的变量的新副本到计划当中。
计划的解决方案所包含的是：一组实例化的行动
变量绑定不仅可以帮助我们追踪所有随新行动引入计划的变量的可能值，还可以包含指定约束说明（一个变量必须和另一个变量的值相等，尽管我们不知道这个值是多少），因此我们可以指定计划中的变量的约束是相等还是不等。
目的：
- 把操作实例转为行动
- 统一行动的效果和另一个行动的前提条件使用的变量，即使得效果和前提条件匹配

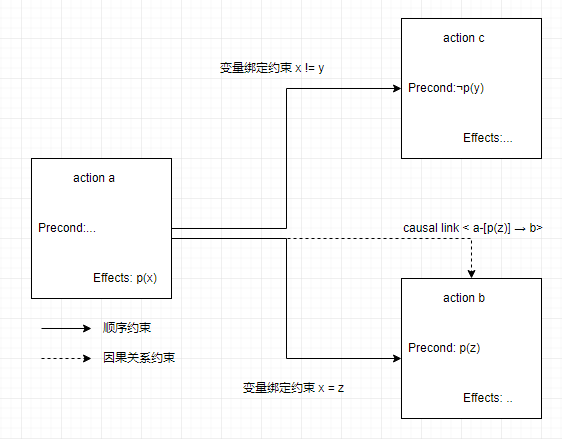
变量绑定的过程如图 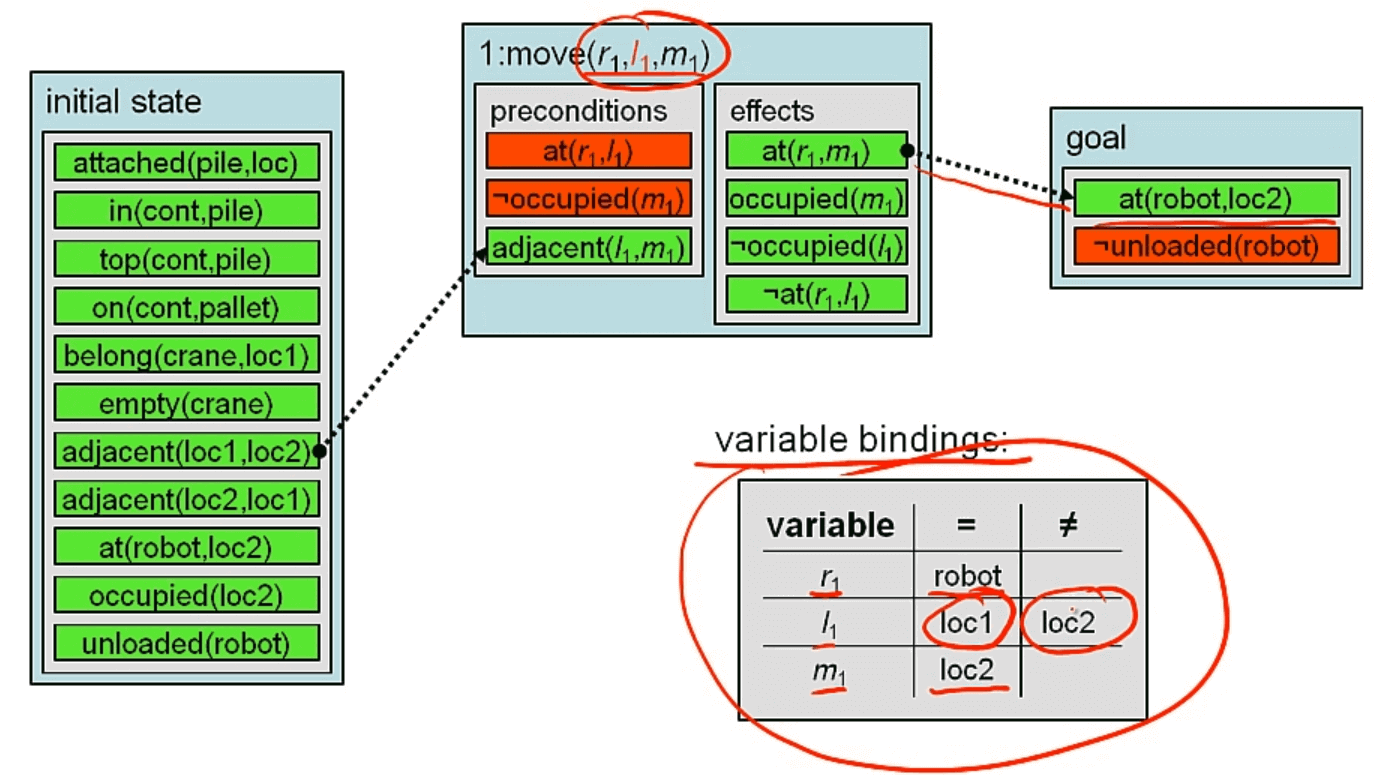image-center 添加行动move,取该行动的id = 1（用来识别该行动的变量），它的变量为，r₁、l₁、m₁

为了满足goal的前提条件at(robot,loc2)，要求move的变量 r₁ = robot，m₁ = loc2，
另外，存在一个威胁（关于什么是威胁后面在仔细说明，选择就理解为可能干扰项）¬at(r₁,l₁),为了排除干扰，则l₁ ≠ m₁ ，即l₁ ≠ loc2。
为了满足move 的前提条件 adjacent(l₁,m₁)，init 中有两个adjacent命题可选项,因为变量绑定约束有l₁ ≠ loc2，所以只能取adjacent(loc1,loc2)
以此类推…

4.添加顺序约束

所有行动必须在初始状态之后
所有行动必须在最终目标之前
因果关系链实现顺序约束（前后）
避免可能的干扰（只有因果关系是不够的，某个行动的效果可能会被其他行动消除，因此，加上顺序约束可以保证在这个行动之后，不会有行动对此效果产生影响）

以上就是四种可能的过渡操作。

计划空间中的搜索

在计划空间中，我们将初始状态和最终目标转换为虚拟行动

init : init (action) 没有前提条件，只有作用效果
goal : goal (action)目标条件作为前提条件，没有作用效果

空计划 π₀ = ({init,goal} , {init ‹ goal},{},{} ):

行动列表A 中包含两个虚拟行动 ,init 和 goal
顺序约束列表包含一个约束，init 在 goal之前
没有变量绑定
没有因果关系

后继函数：通过（一个或多个）计划细化操作来生成后继

添加行动到行动列表A
添加顺序约束到顺序列表 ‹
添加绑定关系到变量绑定列表 B
添加因果关系链到因果关系列表 L

plan-space search 解耦了两个我们需要解决的问题

我们需要哪些行动
我们要如何组织这些行动，构成计划的基础结构是什么

规划空间的搜索原理是，通过不断的细化局部计划，来得到完整的计划。在规划过程中，每一次进行细化操作，我们就把一组可能的计划转为可细化的局部计划，直到该计划完全落实（fully ground），最终得到一个完整计划。

goal test:什么时候停止搜索一个规划，如果他的局部计划不再有缺陷时，该局部计划就是解决方案，因此，我们进行goal-test的指标就是检查一个局部计划，看它是否没有缺陷。

如何判断我们的解决方案中不在有缺陷

在局部计划中，存在两种缺陷

缺陷1：开放目标（Open Goals）
- 最终目标或子目标的未满足，即没有支持某个行动的前提p的因果关系链
- 解决
  - 寻找一个行动b(要么已经在计划中，要么插入计划)，该行动可以用来在行动a之前建立前提p
  - 实例化变量以及绑定变量约束
  - 创建因果关系链
缺陷2：风险（Threats）
- 某个行为的效果可能会影响到因果关系链
  - 如，行动a建立行动b的前提条件p，而另一个行动c可以删除p。如果 c 恰好在 a 和 b之间，则会使得a的效果无效。

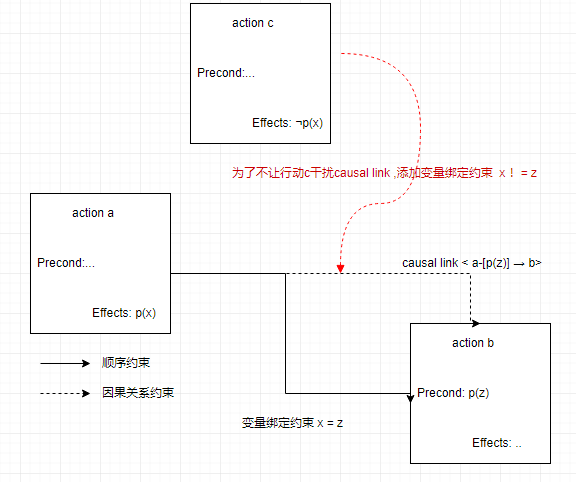
如何解决缺陷

为了防止c删除p而给它添加一个约束，以下有三种方式
- 使b在c之前
- 使c在a之前
- 约束变量，防止c删除p