Ai Plan (09) PSP 算法

by Yimi

November 10, 2019

Categories

• 学习笔记

Tags

• Ai
• 学习笔记

Table of Contents

1. PSP 算法
2. PSP 实现细节
   1. plan.openGoals：寻找未实现的子目标（增量的，即不需要每一次循环都全部重新计算）
   2. plan.threats：寻找潜在的威胁（增量的）
   3. flaw.getResolvers(plan)：获取解决方案
   4. plan.refine(resolver)：细化（改善）计划
3. 管理顺序约束（maintain ordering constraints）
4. 管理变量绑定约束(miantain binding constraints)
5. PSP 的属性:合理性 与 完整性
6. 完整性：对解决方案上的行动数进行归纳

---

PSP 算法

PSP ：Plan-Space Planner 主要原则，在保持顺序约束和变量约束一致的情况下，不断完善局部计划，直到没有缺陷 基础操作：

• 寻找计划的缺陷，即 它的子目标和风险
• 选择一个缺陷
  • 找到所有可以解决它的方式
  • 选择其中一个解决方式，根据该解决方式完善计划

伪代码

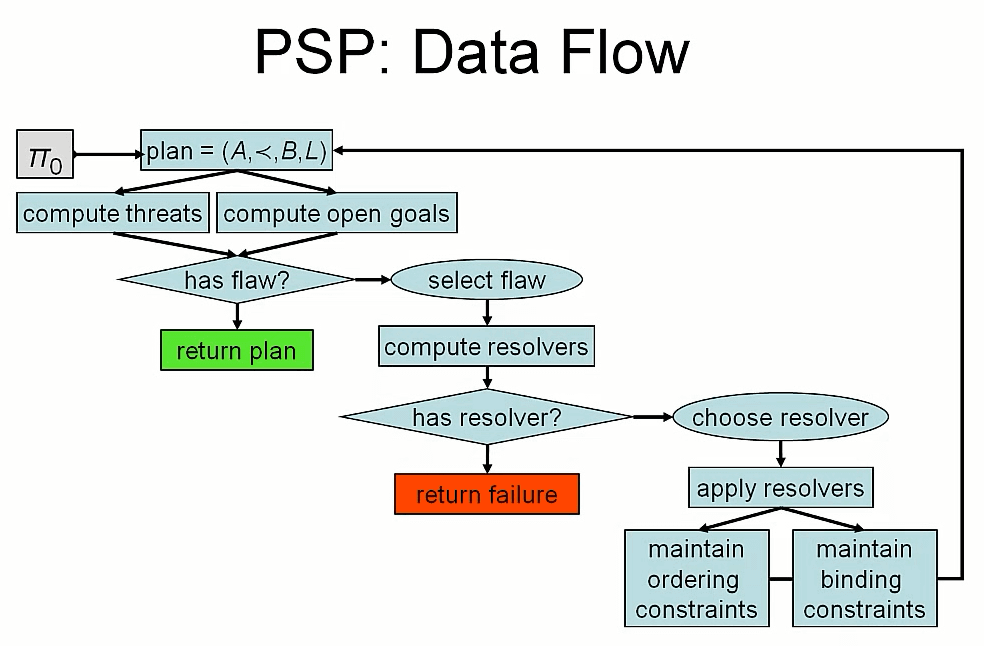
function PSP(plan)
  allFlaws <- plan.openGoals() + plan.threats()
  if allFlaws.empty() then return plan
  flaw <- allFlaws.selectOne
  allResolvers <- flaw.getResolvers(plan)
  if allResolvers.empty() then renturn failure
  resolver <- allResolvers.chooseOne()
  newPlan <- plan.refine(resolver)
  return PSP(newPlan)

需要实现的是

• plan.openGoals：获取所有开放目标，即有前提条件没有被满足的目标
• plan.threats：获取所有威胁 当allFlaws为空是，证明计划已经没有缺陷，因此返回计划
• selectOne：从所有缺陷中选择其中一个
  • selectOne 是确定性选择的
  • selectOne 不需要回溯,在计划成为解决方案前，所有的缺陷都必须解决
  • 顺序对于完整性不重要，不管我们选择先解决哪一个缺陷，都不会影响到别缺陷的解决，因为它们是分层的，而不是平行的
  • 顺序对效率有所影响，如我们选择了一大堆可以解决的缺陷，最后发现了一个不可以解决的缺陷，这是不是前面的都浪费了，反过来，如果我们一开始就发现了一个不可解决的缺陷，就可以立即终止搜索。
• flaw.getResolvers：获取当前局部计划的所有解决方案，当返回空时，说明没有解决方案，返回失败
• allResolvers.chooseOne：从所有解决方案中选择其中一个
  • chooseOne 是不确定性选择的，我们可以使用任意算法来实现，以支持下面的特性
  • chooseOne 需要回溯,当有一个Flaw细化失败，找不到解决方案时，需要回溯，使用别的解决方案
• plan.refine：使用选择的方案来细化计划，继而得到一个新的局部计划
  • 这也是在当前搜索空间生成一个新的搜索节点的步骤

PSP 实现细节

术语说明： 命题：即一组说明世界状态的表达式 前提条件：需要满足的命题 效果：产生一组命题

plan.openGoals：寻找未实现的子目标（增量的，即不需要每一次循环都全部重新计算）

• 在初始计划π₀中，有两个虚拟行动 init 和 goal
• 每次添加行动到计划中时，会把该行动的所有前提条件作为未实现的子目标。因为init没有前提条件，只有goal有，所以goal的所有前提条件都会成为子目标
• 每次条件因果关系链，被保护的命题就不再是未实现的了

未完成的子目标列表会根据新添加的行动的前提条件而增加，而添加因果关系链（实现了前提条件）则会减少子目标列表

plan.threats：寻找潜在的威胁（增量的）

• 在初始计划π₀中，没有如何威胁
• 每次添加行动a_new 到计划 π = (A,‹，B,L)
  • for every causal link < a_i - [p] -> a_j > ∈ L
    • if (a_new ‹ a_j) or (a_j ‹ a_new ) then return
    • else for every effect q of a_new
      • if (∃ σ:σ(p) = σ(¬p)) then q of a_new threatens < a_i - [p] -> a_j>
• 每次添加一个新的因果关系链 < a_i - [p] -> a_j > 到计划π = (A,‹，B,L)时
  • for every action a_old ∈ A
    • if (a_old ‹ a_j ) or (a_j = a_old ) or (a_j ‹ a_old ) then next action else for every effect q of a_old
      • if (∃ σ:σ(p) = σ(¬p)) then q of a_old threatens < a_i - [p] -> a_j>

即，每次添加新的行动或者因果关系链到计划中时，都要检查一下有没有引入威胁，引入威胁的判断是在某个因果关系之间，且恰好有对立命题

flaw.getResolvers(plan)：获取解决方案

• 遍历所有 a_g 中所有未实现的前提条件
  • 在已存在的行动中寻找是否可以联系起来的
    • for every action a_old ∈ A
      • if (a_g = a_old) or (a_g ‹ a_old) then next action
      • else for every effect q of a_old
        • if (∃ σ:σ(p) = σ(p)) then adding < a_old-[σ(p)]->a_g> is a resolver
  • 如果没有，则尝试添加新的行动和因果关系链
    • for every effect q of every operator o
      • if(∃ σ:σ(p) = σ(p)) then adding a_new = o.newInstance() and < a_new-[σ(p)]->a_g> is a resolver
• 遍历所有a_t中威胁到了因果关系链<a_i-[p]->a_j>的效果q
  • 如果满足以下条件，放到因果关系链之前
    • 即a_t不能是生产者(a_t ≠ a_i) ，也不能是a_j 的消费者（(a_t ‹ a_i），如果是，则没有解决方案
      • 如果都不是的话 ，就可以返回 add (a_t ‹ a_i) 作为解决该缺陷的方案（即因果关系链之前）。
  • 放到因果关系链之后
    • 如果 a_t是生产者(a_t = a_i)，或者a_t要先于a_i (a_t ‹ a_i)，就没办法放在因果关系链之后，即没有解决方案。
    • 否则的话，就可以返回add (a_j ‹ a_t) 作为解决该缺陷的方案（即放到因果关系链之后）。

用下面这一张图来说明 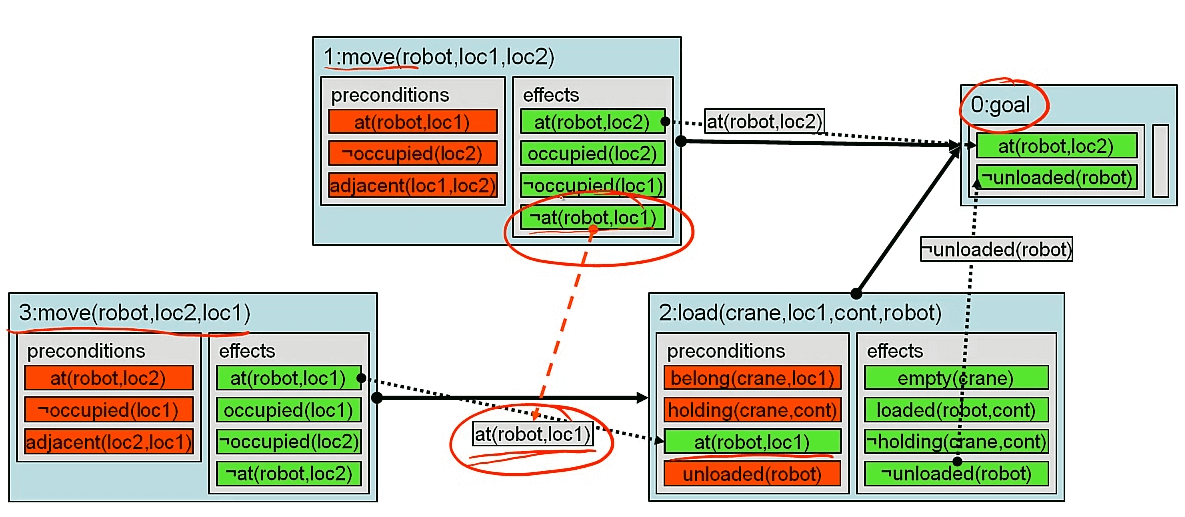1：move，威胁到了 3:move 到 2:load这两个行动的因果关系，如果按照3，1，2，0 来执行，则会失败，因为2的前提条件不满足，被1修改了，因此，只要把1放到2之后，或者，3之前就行了。 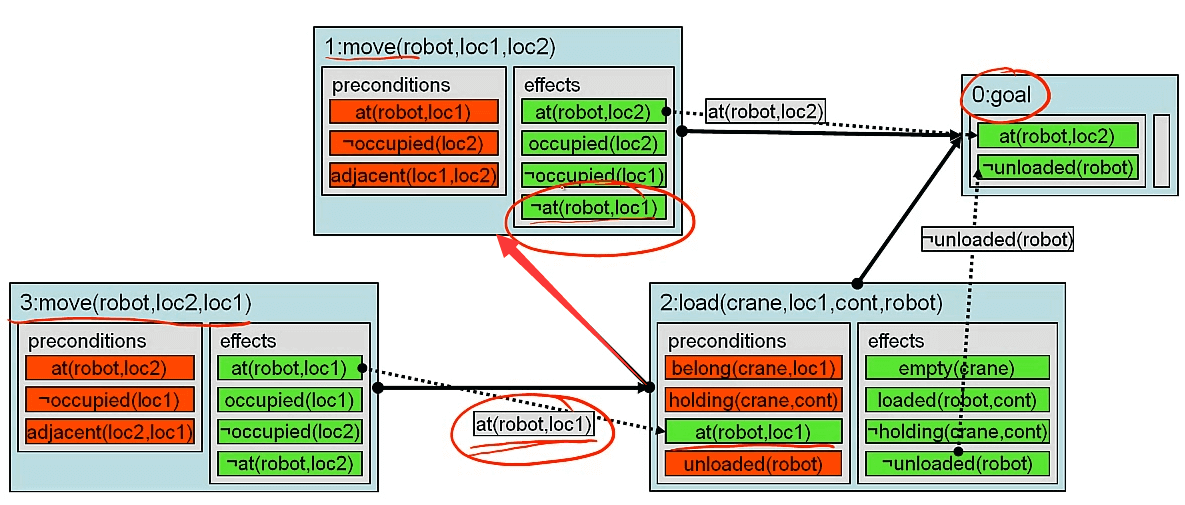同样是a_t中的效果q威胁到因果关系链<a_i-[p]->a_j>,第三种解决方法

• 通过添加变量绑定，让开始时的前提条件检查失败(即约束该威胁命题变量的值,使其不能等于 某个值，来避免其修改该值)
  • for every variable v in p or q
    • if v ≠ σ(v) is consistent with B then
      • adding v ≠ σ(v) is a resolver

原文描述: the other way in which this type of flaw can be resolved is to add variable bindings, such that the unifications that we computed earlier will fail … go to every variable v that occurs in p or q ,and try to make the unification fail on that variable, so if we computed earlier our substitution of v must be a specific value σ(v) , then asserting that our variable v must not have this value is of course a potential resolver, but it is only a resolver if this is consistent with the variable bindings currently in our partial plan, if it is consistent then this is a resolver,adding this variable bindings constraint is a resolver for our flaw

目前对这个方法的描述还不是很迷糊，只记一下当前的理解 σ(v) ，该符号的描述是代入（substitution），表示取变量v的值,返回的可能是单个值，也可能是一组值。然后就是如果 v 的值不为 σ(v)，则它是一个潜在的解决方案，但是，只有和当前的变量绑定一致时，它才是解决方案。这里的“一致”目前有点迷惑，到底怎么样才是一致？ 假设p 为 at(robot,loc1), a3:move(r3,f3,t3)的效果为at(r3,t3)， a1:move(r1,f1,t1)的效果q 为 ¬at(r1,f1), a1的效果威胁到了a3的效果， 为了避免t1影响到t3，

• for every v in at(r3,t3) or ¬at(r1,t1) //遍历两个命题中冲突的变量v
  • 判断v≠ σ(v) 和 B中的一致,如果是，则添加v≠ σ(v)
  • r1 ≠ robot ,不一致，因为已经定义了r1 = robot
  • f1 ≠ loc1 ,一致，因为f1 在 B 中还没有定义，即还没有约束,所以有解决方案
  • r3 ≠ robot ,不一致，因为已经定义了r3 = robot
  • t3 ≠ loc1 ,不一致，因为已经定义了t3 = loc1 最后如果满足,添加变量绑定约束 v ≠ σ(v) （即 f1 ≠ loc1） 作为解决此威胁的解决方案。

变量	=	≠
r1	robot
t1	loc2
r3	robot
t3	loc1

添加绑定变量约束后

变量	=	≠
r1	robot
t1	loc2
r3	robot
t3	loc1
f1		loc1

plan.refine(resolver)：细化（改善）计划

当我们从上一步得到解决方法后，把它应用到当前的局部计划，对其进行细化，即为局部计划添加resolver中指定的元素

• 添加顺序约束
• 添加一个或多个变量绑定约束
• 添加因果关系链
• 添加新行动

然后更新缺陷

• 未实现的前提条件(see: plan.openGoals())
• 威胁（see: plan.threats()）

管理顺序约束（maintain ordering constraints）

需要用到下面两个操作

• 查询 (a_i ‹ a_j),即a_i 是否优先于 a_j
• 添加 (a_i ‹ a_j)

可能的内部表示

• （1）为所给的每个行动维护一组前驱/后继
  • 即 a₀ 没有前驱,后继有a₁，a₂，a₃
  • a₁ 的前驱有a₀,后继有a₂，a₃
  • 以此类推，这种方法就像查字典，缺点是比较占空间
• （2）仅维护每个行动的直接 前驱/后继
  • 这个方法可以取得直接前驱/后继，但是其它节点这需要进行闭包传递计算，才能判断
  • 如，查询a₃ 是不是优先于a₂，则开始计算a₂的前驱a₁，a₁的前驱a₀，最后a₀无前驱，并没有a₃，所以不是
  • 这种方法运行相对比较慢
• （3）维护 ‹ 关系的传递闭包
  • 如 a₀ ‹ a₁，a₀ ‹ a₁，a₀ ‹ a₂，a₀ ‹ a₃，a₁ ‹ a₂，a₁ ‹ a₃，a₂ ‹ a₃
  • 即 a₀ ‹ a₁ ‹ a₂ ‹ a₃
  • 这种方式比价节省，查询起来也比较快，缺点是，添加新的顺序约束时，要计算一遍和相关的全部闭包关系
    • 如增加一个a_n ‹ a₂,则最终会添加 a_n ‹ a₂和a_n ‹ a₃，因为a₂传递了下去

使用哪一种表达式需要在空间复杂度和时间复杂度增加做权衡，因为在规划空间中我们使用比较多的是查询，方法（3）的表示是最好的

管理变量绑定约束(miantain binding constraints)

约束的类型

• 一元约束 ： x ∈ D_x,我们需要只x的值，并且该值必须属于值域D_x
• 二元约束，我们不需要指定x,y的值，只需要它们满足下面条件
  • 等于约束 ： x = y
  • 不等于约束： x ≠ y

一元约束和等于约束比较简单，可以在线性时间内处理完毕。但是不等于约束则会我们带来很多麻烦，因为不等于约束会带来该类型约束网络的指数复杂性。 因此，CSP问题 （constraint satisfaction problem 约束满足问题）一般是 NP-complete 问题。

PSP 的属性:合理性 与 完整性

最终，PSP算法也有了和状态空间规划一样的属性，即合理性（sound）与完整性(complete),意味着，无论何时，如果初始局部计划 π₀可以被完善为一个解决方案，则 PSP(π₀) 会返回一个计划，该计划是合理的，完整的。

证明：

• 合理性： 因为在每一步完善的过程中，我们都遵循了顺序约束和变量绑定 约束，因此可以保证其一致性

• 完整性：对解决方案上的行动数进行归纳

  下一篇，我们将学习PSP算法的改进版本，POP算法（Partial-Order Planning）

Share Tweet LinkedIn Reddit