Ai Plan (11) Task Network

Task and Task Networks
STN Planning
1. 解决方案的定义
2. Ground-TFD 算法

前面我们了解了状态空间搜索和规划空间搜索两种方法，这一次，我们再来认识一种新的方法，分层任务网络，我们不在针对问题来寻找解决方案，而是通过任务来实现某个目标，因为实现目标的方法有许多中，所以，任务的实现方法也有也可以有许多种，根据条件的不同，我们可以选择不同的方式来完成任务，或者无法完成任务（条件全部不满足，没有合适的方法）。下面开始认识分层任务网络的一些相关概念。

Task and Task Networks

Task 以及 Task Networks 是分层任务网络规划（Hierarchical task network planning）中处理的基本组件. 我们从定义简单任务网络开始。

简单任务网络(simple Task Networks)是一种简化的更加一般化的方法，又被成为分层任务网络（HTN,Hierarchial Task Networks）和前面的状态空间和规划空间对比，STN沿用了一些概念，如

术语（terms）:描述定义域中的对象的变量或常量
字面量（literals）:用来表达命题是否正确
Operators:描述我们在定义域中可以执行的行动类型
actions:我们想要执行的操作的实例
state transition function:在执行计划时，世界将如何发生什么变化
plans：规划问题的解决方案

不过，STN还有新的概念

任务(Task):在定义域，我们想要做的事情，简单任务一般直接对应行动，复杂任务一般是无法直接执行的，需要对其分解
方法(Methods):描述完成任务的方式，而该描述一般包含若干个子任务一起实现某些复杂的任务。
任务网络(Task Networks)：这些子任务可以被组织起来，可以彼此之间相互有序，从而形成任务网络

实例说明 使用DWR 堆搬运的例子任务：把一堆集装箱从托盘p₁搬到托盘p₃且保持集装箱的顺序不变 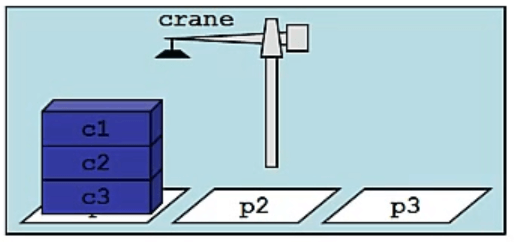image-center 方法定义（非正式的）：

move via intermediate：通过中间（媒介）托盘搬运，把堆搬到中间托盘上（反转顺序），然后再从中间托盘搬到最终目的地（反转顺序）
move stack：重复的搬运最顶部的集装箱到另一个托盘直到搬空，副作用是反转了箱子的顺序
move topmost：每次搬运最上面的集装箱，这个方法先有取得行动，接着是放下行动，这两个行动依照顺序组成了此方法

以上三种方法共同描述了通过层次分解如何把一个堆上的集装箱按照顺序转移到另一个托盘上。

任务（Tasks）

任务符号表(task symbols)： T_s = {t₁,…,t_n},一组符号集，用来标识任务的唯一名称
- 操作名（operator names） ⊊ T_s :基元任务（primitive tasks），操作的名称需要用任务符号表中的符号来命名
- 非基元任务符号： T_s - operator names，那些没有操作名与之对应的符号，成为非基元任务符号，如果有操作的名称与之对应，则称为基元任务符号
任务(task)：t_i(r₁,…,r_k)
- t_i ：任务符号（基元或非基元的），如果是基元符号，说明有总结对应的操作
- r₁,…,r_k：任务操纵的变量/常量，对象
- 实例任务(ground task)：所有的参数都是实例化的，真实的数据，而不是未知的变量
任务和行动的联系，已知action a = op(c₁,…,c_k) ，基元任务t_i(r₁,…,r_k)
- 当且仅当 name (a) = t_i 且 c₁ = r₁,…,c_k = r_k,行动a在状态s下可用
- a 可以在状态s下完成基元任务 t_i

Simple Task Networks 一个简单任务网络w是有向不循环图 (U,E)

U = {t₁,…,t_n}：即U是由一组任务构成的节点集合
E 中的边是 U中的任务的偏序排列（可能不完整的）

如果U中所有任务都是实例的/基元的，那么任务网络w是实例的/基元的；否则，w就是非实例的/非基元的，即只要有一个任务是非实例的，或者非基元的，我们就认为这个任务网络是非实例的，或非基元的

全序STNs

顺序的定义

当存在一条路径从t_u到t_v时，表示在w=(U,E)中,t_u‹ t_v，即t_u先于t_v
如果E 是 U 的全序排列，则 STN w 也是全序的，即
- w 可以用一组这样的任务序列来表示：<t₁,…,t_n>

如果 w= <t₁,…,t_n> 是一个全序的，实例的，基元的简单任务网络，则计划 π(w) = <a₁,…,a_n> where a_i = a_i;i ≤ i ≤ n a_i = a_i 表示行动名称与任务名称相同

实例说明 为更好理解上面的概念，尝试理解一些下面的例子

任务
- t1 = take(crame,loc1,c1,c2,p1); 是基元的，实例的
- t2 = take(crame,loc1,c2,c3,p1); 是基元的，实例的
- t3 = move-stack(p1,q); 是非基元的，因为符号集中不包含move-stack；是非实例的，q是一个变量
任务网络
- w1 = ({t₁,t₂,t₃} , {(t₁,t₂),(t₁,t₃)})
  - 偏序的，t2和t3的顺序没有定义
  - 非基元的，t3是非基元任务
  - 非实例的，t3是非实例任务
- w2 = ({t₁,t₂},{(t₁,t₂)})
  - 全序的，实例的，基元的
  - π(w₂)=
  <take(crame,loc1,c1,c2,p1),take(crame,loc1,c2,c3,p1)>

方法（Method）

我们这次尝试把规划问题当作搜索问题，而Method描述如何改变任务网络的方式，它们用来完善计划，对应于状态空间中的状态转移。 M_s 是方法符号集。一个STN 方法有一个四元组表示 m = (name(m),task(m),precond(m),network(m))

name(m):方法名称
- 语法表示形式为 n (x₁,…,x_k)
  - n ∈ M_s:唯一标志符
  - x₁,…,x_k:方法m中出现的所有变量名称
task(m):一个非基元任务。定义了我们需要完成什么任务
precond(m):方法的一组前提条件
network(m):是这个方法的任务网络(U,E) ，U中的任务被称为方法m 的子任务，可以认为，方法m把task(m)分解为这些组成任务网络的子任务。定义了我们怎样完成任务

有可能有不同的方法来实现相同的任务，方法里使用不同的任务网络以及前提条件。如击杀某个敌人，我们可以使用枪，也可以使用弓箭，或者刀剑，然后什么时候使用什么样的方法，里面具体怎么都不一样。至于方法是全序的还是偏序的，取决于关联的任务网络是全序的还是偏序的。因此，你可以认为，方法，把一个任务分解为若干子任务，并以任务网络的形式表示。

STN Methods 例子

前面的DWR 例子

move topmost的方法，每次搬运最上面的集装箱，该方法定义如下
- take-and-put(c,k,l,p_o,p_d,x_o,x_d)
  - task ：move-topmost(p_o,p_d)
  - precond:top(c,p_o) , on(c,x_o) , attached(p_o,l) , belong(k,l) , attached(p_d,l) , top(x_d,p_d)
  - subtasks:<take(k,l,c,x_o,p_o) , put(k,l,c,x_d,p_d)>
move stack 的方法，重复搬运最顶部的集装箱直到堆为空，因此，需要定义一个递归方法
- recursive-move(p_o,p_d,c,x_o)
  - task: move-stack(p_o,p_d)
  - precond: top(c,p_o) , on(c,x_o)
  - subtasks: < move-topmost(p_o,p_d),move-stack(p_o,p_d) >

no-move(p_o,p_d)
- task: move-stack(p_o,p_d)
- precond:top(pallet,p_o)
- subtasks:<>

上面定义了两种move stack 方法，第一种实现了重复搬运堆中的集装箱的循环，第二种实现确保了递归触及了最后一个。

move via intermediate：通过中间（媒介）托盘搬运，把堆搬到中间托盘上（反转顺序），然后再从中间托盘搬到最终目的地（反转顺序）

move-satck-twice(p_o,p_i,p_d)
- task:move-ordered-stack(p_o,p_d)
- precond: -
- subtasks: <move-stack(p_o,p_i),move-stack(p_i,p_d)>

适用性与相关性（Applicability and Relevance）

方法实例m适用于状态s，如果满足以下条件的话
- precond⁺(m) ⊆ s 且 precond^-(m) ∩ s = {}
- 即m的所有正向前提条件都包含在s中，所有的复兴前提条件都不在s中
方法实例m 和任务t 相关
- 存在一个代入式σ 使得 σ(t) = task(m)
- task(m) 描述了我们通过此方法可以解决什么问题，如果任务网络中有一个任务t，而我们可以使用此方法来代替该任务，并可以使用该方法来完成任务，则方法m和任务t是相关的。

如果任务网络中有一个任务t，以及有一个方法m 和它相关，关系是σ ,则可以通过分解任务来应用此方法

δ(t,m,σ ) ,通过调用分解函数，返回
- σ (network(m)) ，和m相关的实例化的任务网络
- 或者 σ(<subtasks(m)>) ，如果m 是全序的话，就返回这些子任务的序列

适用性和相关性实例

task t = move-stack(p1,q)
state s 如图
方法实例 m_i = recursive-move(p1,p2,c1,c2)
- m_i 在s状态下适用
- 在 σ = {q← p2} 时，m_i 和 t 相关。即当q = p2时，m_i 和 t 相关

分解（Decomposition）

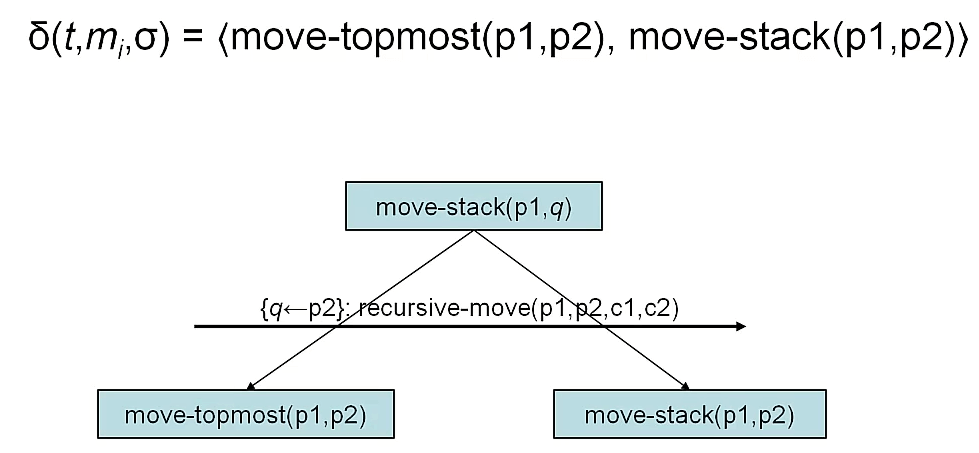
一个简单的分解例子 image-center

假设

任务网络 w = (U,E)
- U = {t₁,…,t_n}：即U是由一组任务构成的节点集合
- E 是排列约束，E中保存的是U中的任务的偏序排列（可能不完整的）
t ∈ U , 且在在w中没有任何前驱节点，也就是说，t是一个根节点
m 是在某种替换σ下和t 在 network(m)=(U_m,E_m)中相关

则，当满足下面条件时，t 在 w 中，通过方法m 在使用替换 σ 得到的分解，是一个简单任务网络 δ(w,t,m,σ)

t 是对U中的该任务使用σ(U_m) 进行实例化并且替换
- 如，U = <move-stack(p,d)> ,经过m = recursive-move(p0,d0,c0,x0) 分解，得到 U = <move-stack(p0,d0),move-stack(p0,d0)>,U 中的任务被实例化并替换掉了。
E中涉及到t的边也被替换成抵达σ(U_m) 中适当的节点的边
- 简单的理解是，把原先的节点间的顺序，修改为变换后的新的的节点间的顺序
- 如，原先是 <t1,t2,t3>,t1 被分解为<t4,t5,t6>,则原先的顺序也应该被替换成<t4,t5,t6,t2,t3>

STN Planning

STN规划的定义域 d = (O,M) 一个STN规划问题可以看做一个四元组 p = (s_i,w_i,O,M)

s_i 是初始状态
w_i 是当前任务网络
O 是定义域的操作集
M 是定义域的方法集

解决方案的定义

如果w_i和定义域d 都是全序的话，那么p 是一个全序STN规划问题对于p= (s_i,w_i,O,M) 的解决方案π =<a₁,…,a_n>

如果w_i 为空，则解决方案也为空
当 t （t ∈ w_i）是一个基元任务,且没有前驱任务时
- 如果a₁ = t 在s_i中可用
- 则，π’ = <a₂,…,a_n> 是 p’= (γ(s_i,a₁),w_i-{t} , O, M)
- 其实就是解决了某个任务，更新当前状态，把该任务从任务网络中移除，开始解决下一个任务
当 t （t∈w_i）是一个复合任务,且没有前驱任务时
- 如果方法m和t相关，即 σ(t) = task(m) 在 s_i中可用
- 则π是 p’ = (s_i,δ(w_i,t,m,σ),O,M)的解决方案
- 其实就是通过方法m替换了原先的任务网络

Ground-TFD 算法

TFP (Total-Order Forward Decomposition，全序正向分解) 伪代码：

function Ground-TFD(s,<t₁,…,t_k>,O,M)
- if k = 0 return <>
- if t₁.isPrimitive() then
  - actions = {(a,σ) | a = σ(t₁ and a applicable in s)}
  - if actions.isEmpty() then return failure
  - (a,σ) = actions.chooseOne()
  - plan ← Ground-TFD(γ(s,a),σ(<t₂,…,t_k>) ,O,M)
  - if plan = failure then return failure
  - else renturn <a> · plan
- else
  - methods = {(m,σ) | m is relevant for σ(t₁) and m is applicable in s }
  - if methods.isEmpty() then retun failure
  - (m,σ) = methods.chooseOne()
  - plan ← subtasks(m) · σ(<t₂,…,t_k>)
  - return Ground-TFD(s,plan,O,M)

这个算法中需要注意的点在处理基元任务时

获取和此任务同名的行动（前面介绍过基元任务，一定对应这与之同名的行动），如果没有，返回失败
从这些任务实例中获取合适，通过chooseOne建立回溯点，当这个行动不合适时，获取下一个
把计划串联起来，通过去掉当前行动，使用γ(s,a)获取该行动之后的下一个状态，递归下去，Ground-TFD(γ(s,a),σ(<t₂,…,t_k>) ,O,M)
就当这个回溯完成了后面所有工作得到了一个计划plan，但是这个计划都是在当前行动之后完成的，所以，把a添加到计划最前面，即<a> · plan。（因为这个算法是全序的，所以这里可以是简单的插入队列最前面）

在处理复合任务时

plan ← subtasks(m) · σ(<t₂,…,t_k>) 是把第一个任务分解为子任务，然后按顺序插入计划的前面，后面的t₂,…,t_k,也全部用σ代入，得到一个新的计划序列，然后把新的计划序列作为参数递归下去。算法的整体思路是，处理首个任务，如果是基元任务，转为行动后添加到解决方案，如果是非基元任务，则分解任务，直到第一个任务是基元任务再继续处理。分解时，因为每个任务都可能有不同方法实现，在使用不同方法时，为了保证前后一致，代入式σ也要应用到其余任务中，即σ(<t₂,…,t_k>)。

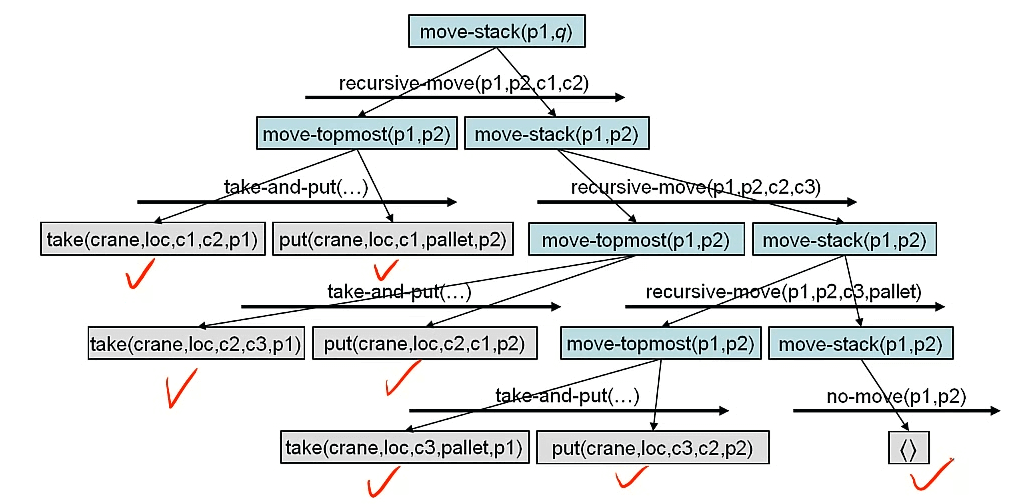
还是使用DWR的例子来分析这个算法 image-center

最开始时，只有一个任务 move-stack(p1,q)
因为这个不是基元任务，所以选择合适的相关方法recursive-move(p1,p2,c1,c2)，分解该任务,σ = (q = p2)，得到两个子任务
- move-topmost(p1,p2),不是基元任务，选择方法take-and-put(…) 分解任务
  - take(crane,loc1,c2,p1),是基元任务，找到对应行动，添加到计划最前面
  - put(crane,loc,c1,pallet,p2),是基元任务，找到对应行动，添加到计划最前面
- move-stack(p1,p2),不是基元任务，选择方法recursive-move(p1,p2,c2,c3)分解任务，得到两个子任务
  - move-topmost(p1,p2) ，…
  - move-stack(p1,p2),不是基元任务，选择方法recursive-move(p1,p2,c3,pallet)分解任务，得到两个子任务
    - move-topmost(p1,p2) ，…
    - move-stack(p1,p2),不是基元任务，方法recursive-move的前提条件不再满足,选择下一个方法no-move(p1,p2)，满足条件，分解得到
      - <> 空集，即什么都不用做