Table of Contents
很早就听说过WFC,但是只知道它是用来随机生成的算法。后来看了一些该算法生成的一些有趣的，漂亮的东西，便开始感兴趣。反正也是闲着，就去看看它到底是一个什么东西吧，了解之后，如果有时间就自己也实现一个玩玩。
规则集
例如我们要创建一个2D的瓦片地图(Tiled Map)，在我们开始创建内容前，首先我们需要准备填充素材，以及明确创建的规则。假设我们有陆地、海岸、海洋三种元素（当然实际创作过程中不止三种，可能还有山脉，荒漠，雪地，雪山等等，不过为了避免问题变得复杂，就拿最简单的来进行说明，等理解后就可以自由发挥和扩展了）
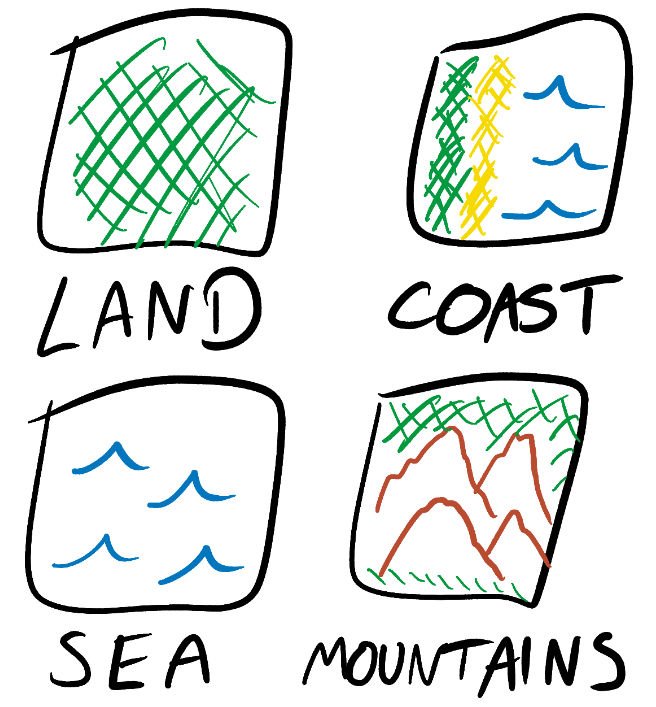
然后它们可能会有一些规则，例如“陆地可以贴近海岸”，“海岸可以贴近海”，“海可以贴近其他海”。
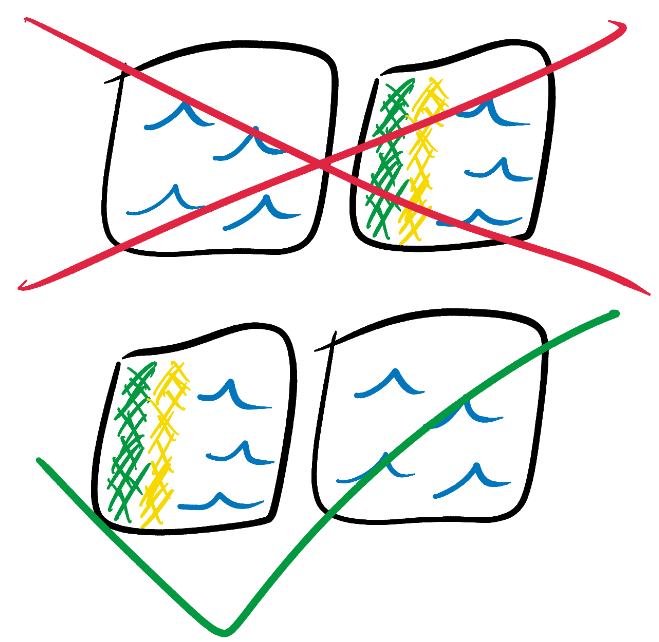我们可以将这些元素进行对称和旋转处理来满足规则，但也会使得代码变得复杂。
简单的规则就像（Sea,Coast,Left）这样一组三元组，它表示了海可以放在海岸左边，不过这条规则需要伴随着另一条从海岸角度来描述的规则，即（Coast,Sea,Right）。如果还想海可以放在海岸右边，就需要继续添加（Sea,Coast,Right）和（Coast,Sea,Left）。不过我们不用手动创建所有这些规则，我们可以通过给WFC提供一些示例，它会自动解析它们来生成规则集。
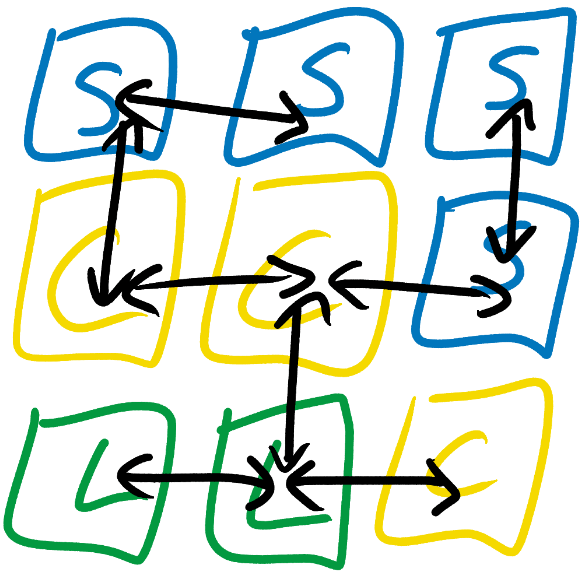另外，他还会分析每种元素的出现频率。这个会在后面的波函数处理时，作为选择使用哪个元素的权重依据。
有了这些准备后就可以开始着手构建和坍缩来输出结果了。
坍缩（Collapse）
波函数坍缩经常提到的一个例子，薛定谔的猫，在你观察到一个东西前，你不知道他到底处于什么状态，就像黑盒子里的猫，你不知道它是死的还是活的，但是在你观察到之前，它处于重合的状态，但是，在你打开盒子之后，它只能是其中一个结果。
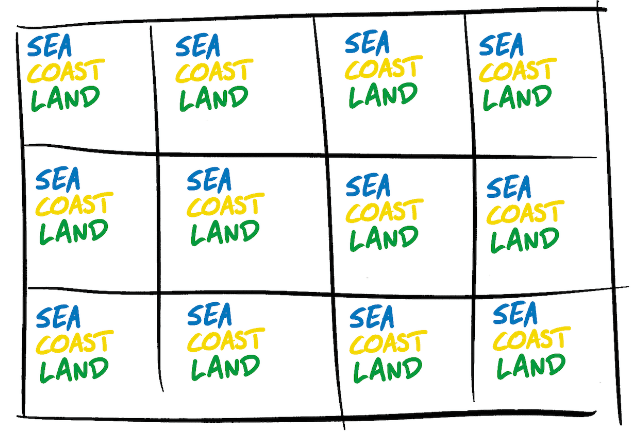
如图，某个格子的状态都是未确定的，可以是三种状态中的任意一个。然后使用波函数开始坍缩处理。先随机选取开始点，每当确定一个格子，会相应的减少邻近格子的波动（即减少这些格子中某些元素出现概率），然后我们再从所有格子中找出熵最低的（也就是比较稳妥的，确定的）格子，来确定其内容（又叫最小熵试探法），确定其内容后又会影响其他格子，就这样一直重复下去，直到波消失（可以联想成涟漪，从某处或多处开始，向外扩散，最后又趋于平静）。最终，波函数坍缩完毕并返回结果，又或者是遇到矛盾返回错误（这种情况可以全部抛弃重新开始，或者回溯丢弃某一步接着继续）。
最终，我们得到了一个世界（或者一个错误）
Shannon Entropy (香农熵)公式，熵表示体系混乱程度
# Sums are over the weights of each remaining
# allowed tile type for the square whose
# entropy we are calculating.
shannon_entropy_for_square =
log(sum(weight)) -
(sum(weight * log(weight)) / sum(weight))
参考资料