0. 什么是规划
什么是规划?或者说,什么是AI规划?
AI 规划简单来说,就是通过预计行动的结果来选择来组织一个明确的,合适的行动计划的过程
1. 规划的概念模型
为了帮助我们定义问题,不妨把规划看作一个状态迁移的系统 ∑ = (S,A,E,γ),状态迁移系统包含四个组成部分,这四个组成了我们通常提到的问题定义域:
- S = {s1,s2,…}:States世界中所有的可能状态的合集,该合集可能是有限的或者无限递归的
- A = {a1,a2,…}:Actions是代理可以执行的行为,从而改变世界的状态
- E = {e1,e2,…}:Evens是世界中发生的事件,不受任何代理的控制,事件也可以改变世界的状态
- γ: S x (A ∪ E)→ 2S:状态转移功能是状态转移系统中最复杂的组成部分,该公式表示获取世界状态的输入以及(行为或事件),→表示过渡到另一个状态集
举例: if(a ∈ A) 且 γ(s,a) ≠ Φ,则a 适用于当前的状态s,在当前状态执行a会将系统转移到 s’∈ γ(s,a)
1.1 用图表示状态迁移系统
状态转移系统 ∑ = (S,A,E,γ) 可以用一个有向标记图 G = (NG,EG) 来表示。
- 每个节点对应S集合中的每个状态,即 NG = S
- 弧从s ∈ NG 到 s’ ∈ NG,即 s-> s’ ∈ EG
- 弧上面的标签u ,u ∈ (A ∪ E),其含义是 s’ ∈ γ(s,u) ,即s’是 u在s中应用的结果。
1.2 计划与目标
- 状态转移系统描述了系统所有可能的发展情况
- 计划
- 一个给出用来实现从某个状态到目标状态的一些适当行为的结构
- 一个简单的,常见的结构是一个有序的行为列表,我们需要按顺序来执行
- 另一种复杂的结构是状态到行为的映射的功能,我们可以使用该功能来确定要采取哪个行动
- 一个给出用来实现从某个状态到目标状态的一些适当行为的结构
- 目标
- 最终目标:可以是具体的某个状态 或者是一组状态
- 约束:状态可能包含某些约束,需要满足条件才能达成,从而避免我们不希望出现的状态
- 效用优化函数:复杂点的目标可能还需要某些辅助功能,来最大限度地提高我们的效用
- 任务的表现:规划过程不需要实际去实现具体行为
1.3 规划与执行计划
- 规划器(Planner)
- 输入: 状态转移系统(descript of ∑),初始化状态(initial state),以及目标(objective)
- 生成:达成目标的计划
- 控制器(Controller)
- 执行计划中的行为,因此它需要提取下一个需要执行的行为传递个系统,行为的执行改变了我们当前系统的实际状态,通过观测函数(计划监督),它会观测每个状态。当执行行为后,观测到的值与预期值不一样,那么就需要计划修订或者重新规划
- 输入:计划,当前状态(观测函数 η = S→ O)
- 生成:行为(action)
- 状态转移系统(state-transition system)
- 随着动作的执行和事件的发生而发展
规划与调度
规划
- 决定使用哪些行动来实现某些目标
- 可能比NP-complete 糟糕,最坏的情况是不确定的 Scheduling
- 决定什么时候已经怎么样执行一组动作
- 时间限制
- 资源限制
- 目标功能
- 典型的 NP-complete
2.规划与搜索
我们把问题分为Toy Problems 和 Real-World Problems
- Toy Problems
- 简明扼要,常用来说明目的,或者用来比较不同算法的性能;
- 多样性:可以是任何琐碎的事情
- 简单:可以轻松准确的描述
- Real-World Problems
- 没有一个可以准确描述的定义,即对同一个问题,每个人的描述方式都可能不一样,描述这个问题是什么,以及有哪些细节需要注意。
- 人们关心的是解决方案
2.1 搜索问题
我们可以把规划问题转化为一个搜索问题,搜索问题可以由下面四个部分组成
- 初始状态(initial state)
- 一组可能的行为或合适的条件(successor funtion)
- 后继函数: 把state映射到一组<action,state>对,即该状态可以执行的动作以及执行该动作后的状态
- 状态空间:后继函数+初始状态 = 状态空间
- path(解决方案,一条指出从初始状态到目标状态的路径)
- 目标(goal)
- 可以是某个目的的状态 或者是用来验证是否达成目标的函数
- 路径成本 函数 (path cost function)
- 用来优化
- 假设:路径成本 = 每一步的成本
2.2 问题表述
- 决定要处理什么样的行为和状态需要考虑的过程
- 粒度或抽象的层次
当我们描述某个问题时,我们会做以下假设
- 环境的假设
- 有限以及离散的(discrete)
- 完全可观察的,当前世界所有相关的状态都可以被规划算法获取
- 确定性的(deterministic),所有的行为都是有明确定义的输出,而非模棱两可的
- 静态的,即没有事件,所有什么都不会发生,只有我们执行的行为才会影响世界的状态。
- 其它假设
- 受限的目标:要么是一单个状态作为目标,要么是一组状态作为目标
- 有序的计划:不考虑并发的情况
- 隐性时间:即activity不会有持续时间,即无视某个活动执行所需时间
- 离线规划:执行规划时,外部的世界不会发生变化(即我们取得当前世界状态的副本,作为计划时的参考)
2.3 搜索节点的数据结构
在开始学习搜索算法前,首先了解一下搜索所需的数据结构
Search Nodes: 搜索树中的节点
- 数据结构
- state
- parent node:该节点在搜索树中的直接前继节点
- action:从父节点到该节点所需的行为
- path cost:抵达该节点所需要的总成本
- depth :该节点在搜索树中的深度
2.4 通用树搜索算法
//fringe : 边缘,有时也记为 openNodesSet。开放节点集,即未处理的节点集合
//相对的,closeNodesSet,已经处理,探索过的
function treeSearch(problem,strategy)
fringe <- {new searchNode(problem.initialState)}
loop
if empty(fringe) then return failuer
node <- selectFrom(fringe,strategy)
if problem.goalTest(node.state) then
return pathTo(node)
finge <- finge + expand(problem,node)
分析上面的伪代码,我们拥有一个树搜索函数:
- 传入是一个问题描述以及一个策略
- 创建一个根节点,然后把它放入开放节点集
- 检测开放节点集是否为空
- 如果是,则说明我们把所有的节点都找遍了也没找到目标节点,搜索失败,退出
- 如果不是,从开放节点集中,依据策略选择一个最优节点
- 判断该节点是否为目标节点
- 是,表示已经找到一个解决方案,返回到达该节点的路径
- 不是,根据问题拓展该节点(获取该节点的所有后继节点),更新开放结果集,返回第三步
- 判断该节点是否为目标节点
注意:
- pathTo(node):因为每一个节点都记录着自己的直接前继节点,所以只需要倒叙遍历回去就可以得到抵达目标节点的路径
- 注意无限循环的可能性,即使节点有限,也可能导致无限循环的出现,如A->B,B->A,当A和B都不是我们需要的结果时,就会产生无限循环
2.4.1 搜索控制策略/ Search (Control) Strategy
控制策略是一种用来调度(安排)后继节点的有效方法
- 从开放节点集中选择下一个测试节点
- 确定节点的扩展顺序
- 目的:尽可能快速的得到目标状态
例如:
- 用LIFO / FIFO 队列保存开放节点集
- LIFO 后进先出,表示我们总是访问到最新添加到队列里的节点,即深度优先搜索
- FIFO 先进先出,表示安装加入队列的时间顺序进行方法,即广度优先搜索
- 按字母顺序
- Heuristic 启发式
在把具有重复状态的搜索树转换为图搜索时,记得使用哈希表记录已经探索过的节点,也可以减少遍历是产生的消耗。在检查开放节点集时,先检查该哈希表是否已经遍历过,如果是,则跳过。
3 练习例子
有兴趣和时间的话,可以练习以下下面的例子,尝试分析以下这些问题的States和,Actions,以及如何抵达目标状态
3.1 传教士与食人魔
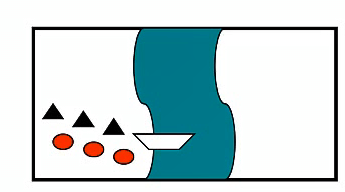
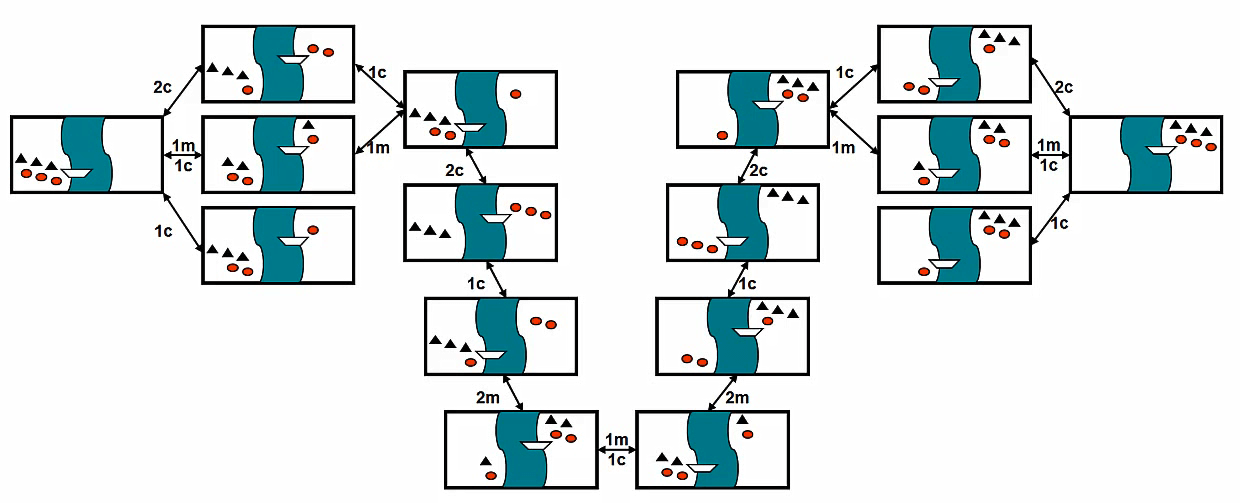
- 问题描述:
- 目的:把所有人都安全送到和对面
- 条件
- 当食人族的人数多于传教士的人数时,传教士会被吃掉
- 小船最多可以载两个人
3.2 滑块拼图
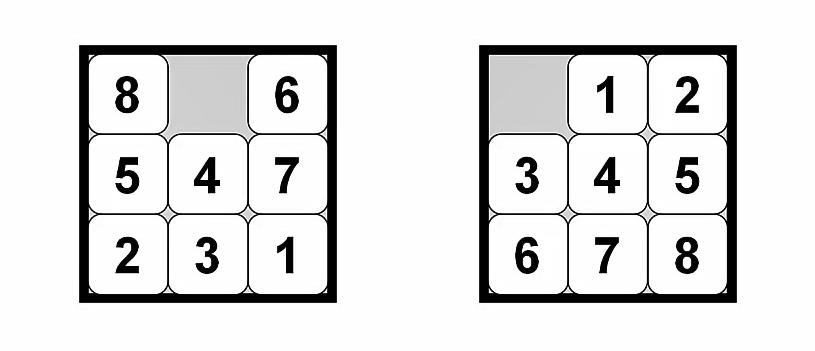
- 问题描述:
- 目的:把左边的拼图变成右边的状态
- 条件
- 只能移动空格周围的格子
- 高级点的版本如4x4或并5x5,问题的规模也随之增加
- 更加有趣点的例子如华容道,相信玩过的小伙伴都对它有点印象吧
3.3 N皇后
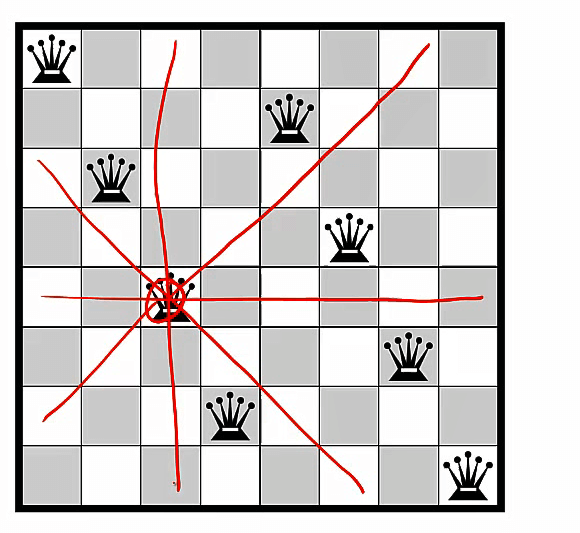
- 问题描述:
- 目的:在8x8的棋盘中放置8个皇后,使她们都无法攻击到彼此
- 条件
- 皇后的攻击范围如图所示,是个米字型


