Table of Contents
名词说明 fringe ：等待处理的节点列表，又称为 openlist ,即未探索的节点，相对的，有closelist
Breadth First Seardh (广度优先搜索)
最简单暴力点方法,遵循先进先出（FIFO） 前向 状态空间 搜索算法(Forward State-Space Search Algorithm)
function fwd_Search(O, S_i , g )
state ← S_i
plan ← <>
loop
if state.satisfies(g) then return plan
applicables ← { ground instances from O applicable in state }
if applicables.isEmpty() then return failure
action ← applicables.chooseOne()
state ← γ(state,action)
plane ← plan • <action>
对该伪代码进行分析
- 步骤-1 输入 操作（Operator = preconditions + effects ,前提条件和效果） ，当前状态，目标状态
- 步骤-2 创建初始状态
- 步骤-3 创建一个空的计划
- 步骤-4 目标测试：判断当前状态是否满足最终目标
- 是，返回 计划
- 不是，生成当前状态下所有适用的动作的列表
- 适用动作列表是否为空
- 是：返回失败
- 不是
- 选择合适的动作
- 通过当前状态与该动作推进计划得到新的状态
- 把该行动加入计划，回到步骤-4
- 适用动作列表是否为空
Dijstra Algorithm （迪捷斯科拉算法）
是为了解决最短路径提出的算法，前面的广度优先搜索虽然可以得到一条路径，但往往不是最优的。
- 步骤1 假定每个节点之间的距离为他们的成本，每个节点记录着当前路径（即当前的前继节点到自身）所需成本
- 步骤2 从起始点s开始，获取邻近节点，初始化他们的成本= cost（s,n_i），然后这些邻居节点全部添加到fringe 中，s添加到closelist中
- 步骤3 fringe 适用动作列表是否为空
- 是，搜索失败
- 步骤4 从fringe 中获取当前节点n，获取邻近节点，
- 判断是否为目标点
- 是 ，返回路径
- 不是，则判断成本是否初始化，执行完下面后返回 步骤3
- 还没初始化，则初始化他们的成本= n + cost（n,n_i），然后添加到fringe 中
- 否则，计算 newcost = 该节点成本 + 到自身所需成本 ，如果 newcost < 自身目前的cost,则修改前继节点为该节点。
- 判断是否为目标点
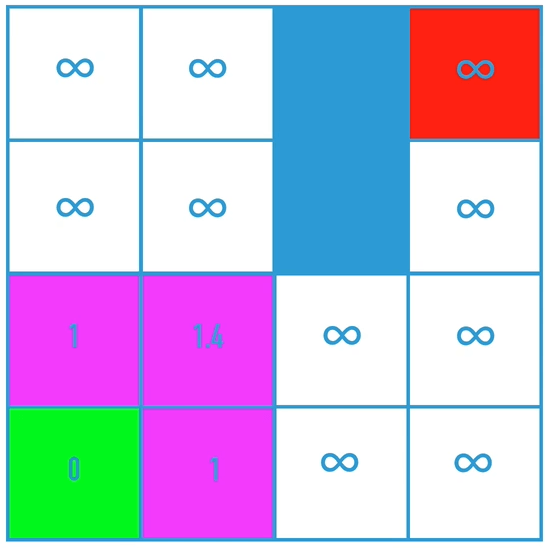
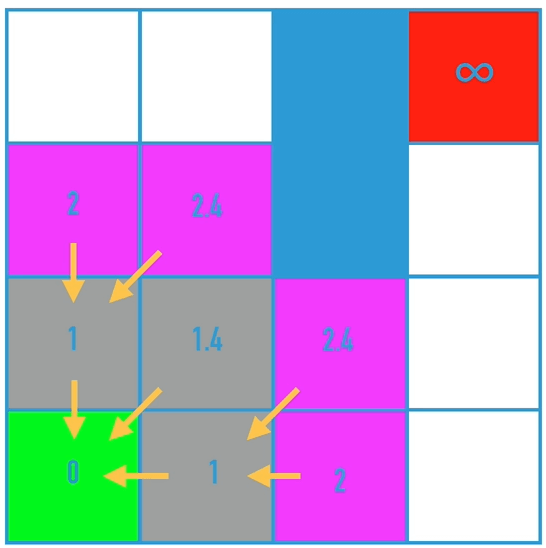
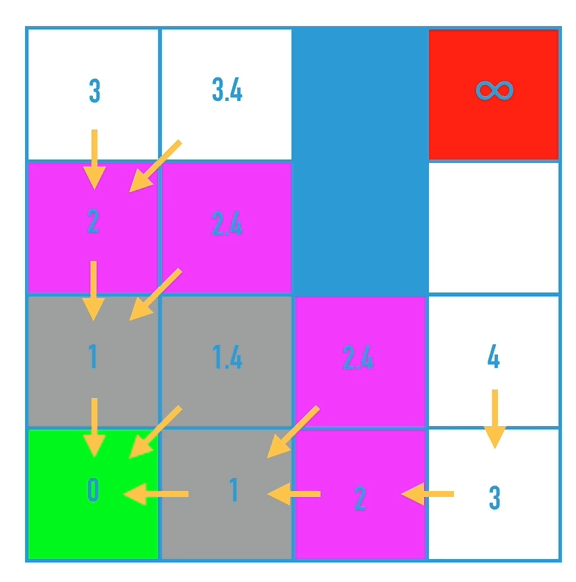
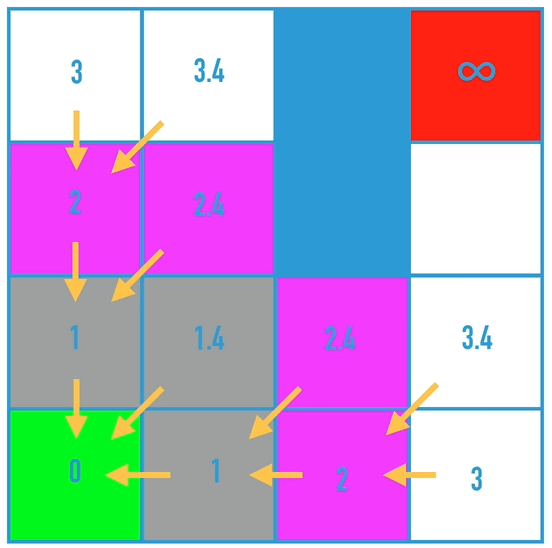
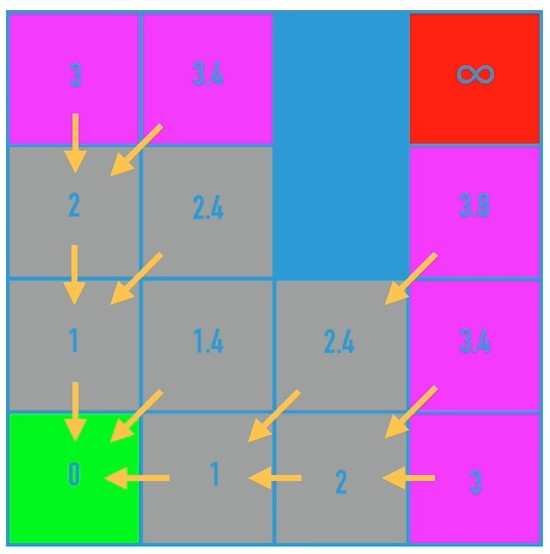该算法的核心是，判断是否有成本更低的邻近节点，如果有，把前继节点改为该节点，最终得到目标点时，倒序遍历就可以得到最短路径
启发式搜索策略
定义：启发式函数 H(n) = 获取从给定节点 n 到目标点成本最低的路径 （如果n 为目标点，则 H(n) = 0） 启发函数是基于特定问题实现的，即不同的问题可能有不同的启发函数。但不管问题的状态空间是什么，启发函数总是可以给我们提供每个状态的数值。一个完美的启发函数应该总是可以给出到目标点的准确最短距离（然而，想要得到完美的启发函数并不现实）。
Best-First Search (最佳优先搜索)
评估函数f 告诉我们以什么样的顺序从fringe中获取节点，前面的方法都只是单纯的先进先出 是一种广度优先树搜索（或图搜索）算法
- 策略：基于评估函数f 选择下一个 探索节点，选择的节点值为 f(n) 的值最小
- 实现：selectFrom(fringe,strategy)
- priority queue (优先队列):通常会把fringe实现成一个以f函数计算的值大小的为顺序的优先队列。即，对我们扩展节点时，把该节点的所有后继节点通过使用f函数进行评估后添加到priority queue，该队列会自动根据前面计算的值的大小，对队列内部的元素进行从小到大的排序，然后选择节点的时候，直接获取队头元素即可（Best-First）。
- priority queue 的实现，可以实现为一个二叉树，在频繁的既要添加节点和又要搜索最小节点的情况下，时间复杂度最简单的实现就是用二叉树进行实现
- priority queue (优先队列):通常会把fringe实现成一个以f函数计算的值大小的为顺序的优先队列。即，对我们扩展节点时，把该节点的所有后继节点通过使用f函数进行评估后添加到priority queue，该队列会自动根据前面计算的值的大小，对队列内部的元素进行从小到大的排序，然后选择节点的时候，直接获取队头元素即可（Best-First）。
下面介绍两种最佳优先算法
1. Greedy Best-First Search(贪婪最佳优先)
使用启发函数作为评估函数： f(n) = h(n)
- 总是优先扩展离目标点最近的节点
- 之所以称为贪婪，是因为它总是获取
- 由于它只是考虑当前最优，不一定能够得到最优路径
- 优点：评估计算成本低（例如，在寻路时只是计算两点间的曼哈顿距离）
- 缺点：局部最优不一定是全局最优，很有可能会得到不理想的路径（远比最佳路径长），总体成本高
2. A* 算法
简单了解 A* (Best-First) Search
先看罗马尼亚旅游问题（Touring Romania）
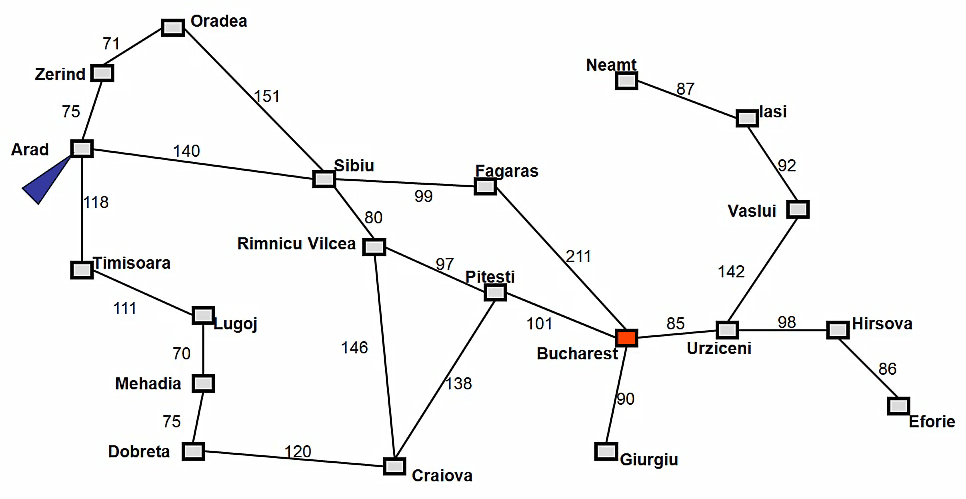假设我们的起始点在阿拉德（Arad），目的地是布加勒斯特（Bucharest）
A* 生成一个搜索树
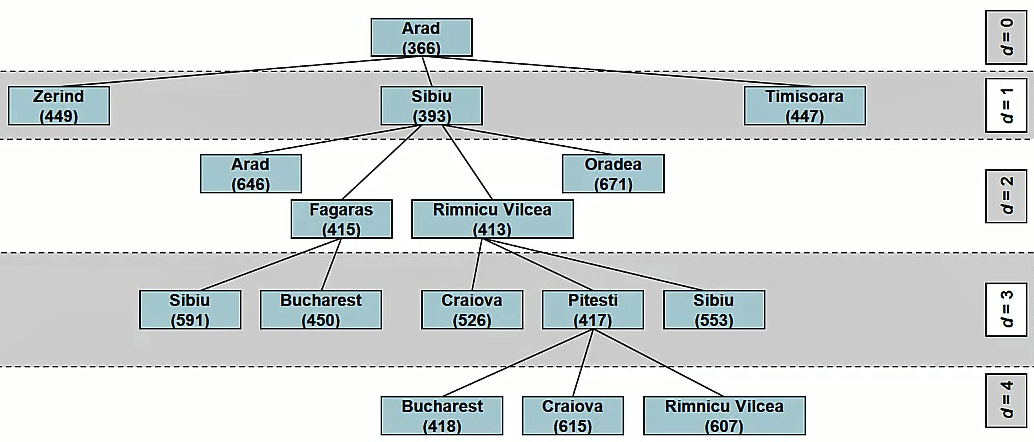A*使用数字来引导搜索，这些数字当前节点与目标节点的h(曼哈顿距离)+g(上一个节点到这个节点的成本)，这被称为启发式。
启发式是用来评估下一步应该扩展哪个节点的算法。
由于贪婪最佳优先算法的短视弊端，人们又对该算法进行改进，从而可以得到真正最佳子节点 它改进了评估函数 f(n) = h(n) + g(n)
- h(n) 和前面一样的启发函数
- g(n) 抵达该节点所需的成本。
- 注意，它会累计前继节点的成本，即A->B 和 C-> B ,B点的成本是不一样的
- 树搜索的话不会有这种合流节点，图或网格的话就需要考虑上述情况
function aStarSearch(problem, h)
fringe ← priorityQueue(new searchNode(problem.initialState))
//allNodes ← hashTable(fringe) // allNodes 用来保存已经探索过的节点的集合
loop
if empty(fringe) then return failure
node ← selectFrom(fringe)
if problem.goalTest(node.state) then
return pathTo(node)
for successor in expand(problem,node)
//if not allNodes.contains(successor) then // 需要测试该节点是否已经探索过
fringe ← fringe + successor@ f(successor) // 将后继节点通过f函数计算后加入fringe , f = g + h
//allNodes.add(successor) // 探索完毕后，添加到已探索节点集合
此伪代码表示A* 的树搜索算法，加上被注释的3行代码后便是图搜索。但是，该算法的图搜索版本有一个问题，就是无法再保证结果是最优路径。 原因出在第2段注释那里，因为我们不在比较已经探索过的节点。但是，和迪捷斯科拉算法一样，某个已经探索过的节点抵达当前点的成本可能会更低。 所以，我们更加关心的，是路径更短的节点，而不是是否已探索过该节点。 因此，我们可以简单的添加一个测试函数，来判断这个已探索过的节点的路径是否比当前路径的成本更低（路径更短）。 不过，一般我们的启发函数也没有那么的准确，所以，得到的路径也不一定就是最佳路径。
空间复杂度，O(bl) 是指数的，意味我们具有指数的时间和空间复杂度
- b 是每个节点平均获得的成功次数
- l 是是我们要查找的路径长度
A* 算法的属性
一个可接受的启发函数h(n)应该满足以下条件
- 永远不会高估 从n 点到最近目标点的距离，即 h(n) <= 实际距离
因此，A*中，如果启发函数是可接受的，则f(n)永远不会高估通过n点到达目标点的成本
- 属性
- 如果树形的A*是最佳的，则启发式是可以接受的。（这里的最佳是指该启发式确保算法能够找到从初始状态起到目标节点的最短路径）
- 同理，如果启发式是可接受的，则A*将返回最佳路径
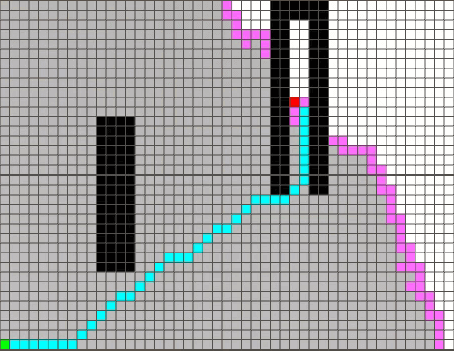
- 当A*完成时，表示有解决方案。可以使用成为轮廓的东西来显示该解决方案
- 轮廓可以观察该算法的执行过程，也表示了在一定成本内达到的状态集。（它有点像我们以前看到的地形高度图，图中的轮廓线表示f值相等的节点，地形图的轮廓线表示高度相同的区域）
- 如果树形的A*是最佳的，则启发式是可以接受的。（这里的最佳是指该启发式确保算法能够找到从初始状态起到目标节点的最短路径）
理论上，A是最好的，它总是可以找到最佳解决方案。它是最高效的，它不会扩展更多非必须的节点。 不过A也不是所有的问题的答案，尤其是图的搜索。
几种算法的对比
好的启发式
前面一直在提好的启发式，那什么样的启发式才是好的启发式呢？ 首先，看一下启发式的定义：
在前面的场景中，我们把启发式定义为估算初始点到目标点的距离点函数。这有点口语化。 那么我们来术语化点的。 启发式是一种准则或方法，用来决定在几种替代方案中选择对实现目标最有效的行动。 现实中的例子：
- 选择成熟的水果。
- 选择哪一门课程进行学习
所以，简单来说，启发式只是一种用来决定哪一种选择看起来最好。如果该决定是正确的，我们就有了一个不错的启发式！
接下来，就是好的启发式
- 减少需要估算的状态的数量
- 可以帮助获取在合理时间内的解决方案。 权衡
- 简单：使用一种简单的方式来区分后继节点，从而减少计算所需时间。但是，简单的方式通常不太准确
- 准确：无法保证一定可以得到最佳的行动方案，但是通常都可以得到准确的
我们怎么样才能找到一个好的启发式？
是不是可以自动生成一个这样的启发式？
- 答案是，Yes!但是，这会非常复杂。自动找到好的启发式也是过去10~15年中关于AI规划研究最热门的主题之一。
- 其想法是基于放宽问题
- 问题通常是根据状态定义的，行动则是在后继节点实现某些目标
- 即删除原问题的某些限制,得到一个行动上比原问题更少限制的新问题
- 被放宽的问题的最佳解决方案对于原问题来说是一个可接受和一致的启发式。 这里就不再深入了，了解一下就好。
例子
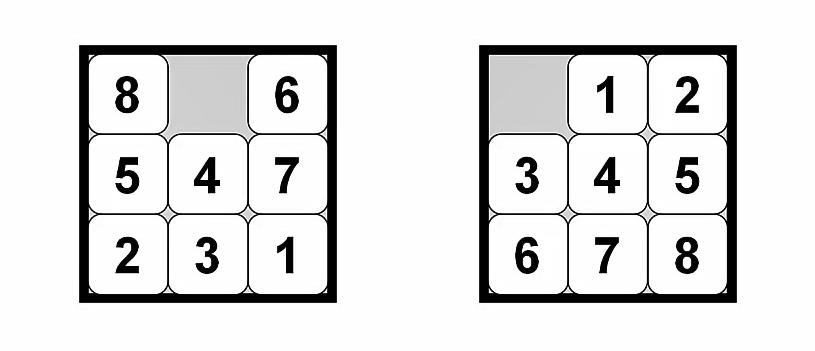思考之前的拼图问题，可不可以给它设计启发函数呢？
答案是可以的！
- h1:放错了位置的数字的数量
- h2:格子的曼哈顿距离 dis = dx + dy ,即与目标点水平(x)距离 + 与目标点垂直（y）距离
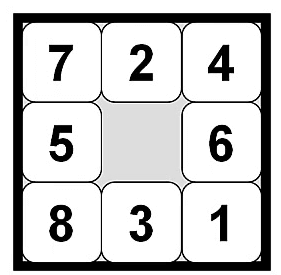例如上图的情况：
h1 = 8 (8个数字都放错位置了) h2 = 3 +1 +2 + 2 + 2 + 3 + 3 +2 = 18
内存一般可以允许3x3的网格的搜索空间。
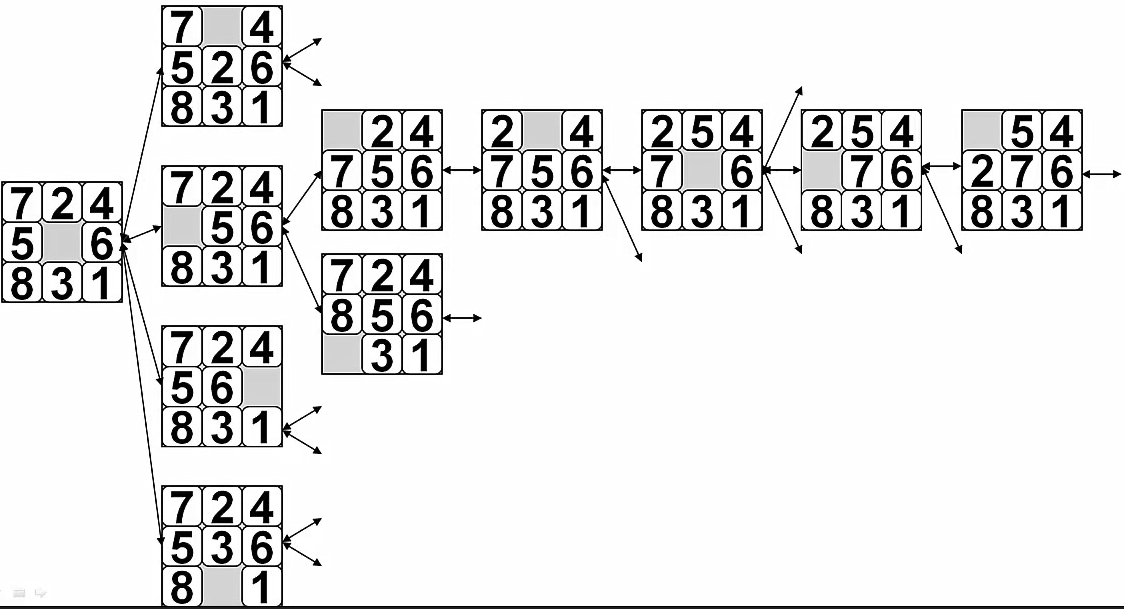状态太多放不下了，可以看一下这个问题所需的空间，随着遍历的深度增加，状态的数量呈指数增长。
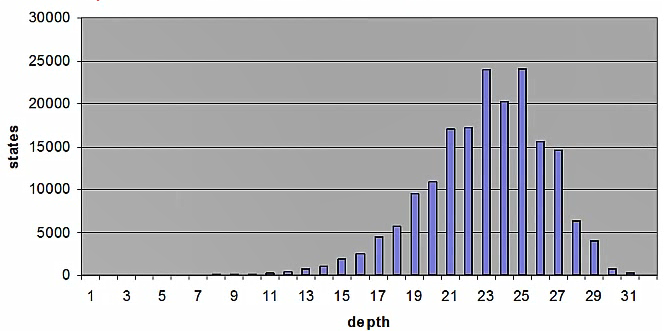
如果是树搜索的话，在深度24那里它还会继续指数增长。这里是图的搜索，所以并没有树搜索的那么可怕，但是图搜索也需要付出一些代价，那就是需要维护一张哈希表来记录已探索的节点，以及比较表中的状态，有时这个表也会占很多空间