Table of Contents
PoP (Partial-Order Planning)
PoP 是 PSP的的一种实现。 在PSP算法中,我们考虑了两种缺陷:未实现的目标和威胁,并每次在主循环消除这些缺陷。而POP只考虑未实现的目标,而把处理威胁放在主循环中。
如图,这张图只是前面的PSP算法上做一些修改,把威胁放到opengoals处理完毕后,在主循环把所有因为opengoal resolver导致的威胁处理完毕
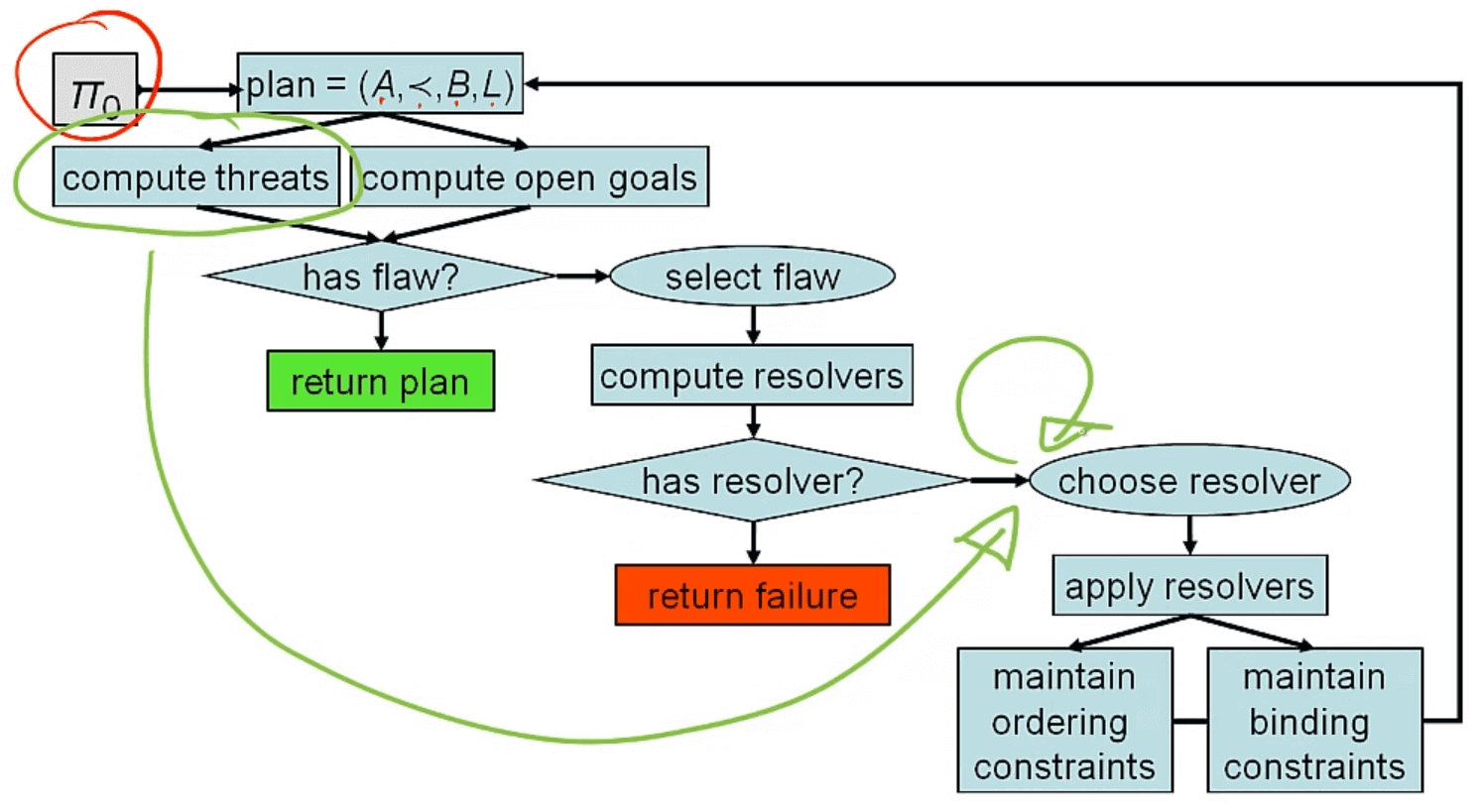
PoP的输入
- partial plan (和PSP的一样)
- agenda(议程):即需要完成的事,是一组 形如(a,p)组合,a表示行动,p表示该行动的某个前提条件。因此,这些就是当前局部计划中的所有开放目标
- 初始时,它是虚拟行动goal的所有前提条件
- 议程只是避免了我们每次循环都重新计算open goals 的一种方式。
- 搜索由缺陷类型控制
- 未实现子目标(在agenda中):和前面PSP算法一样
- 威胁:作为生成后继的一部分来处理来解决
- 在算法中,我们消除了所有的威胁,因此,当我们生成一个新的搜索节点时,它将没有任何威胁。
伪代码
- function Pop(plan,agenda)
- if agenda.empty() then return plan
- (ag,ap) ← agenda.selectOne()
- agenda←agenda - (ag,ap)
- relevant ← plan.getProviders(pg)
- if relevant.empty() then return failure
- (ap,pp,σ) ← relevant.chooseOne()
- plan.L ← plan.L ∪ <ap-[σ(pg)]→ag>
- plan.B ← plan.B U σ
- if ap ∉ plan.A then
- plan.add(ap)
- agenda ← agenda + ap.preconditions
- newPlan ← plan
- for each threat on <ap-[σ(pg)]→ag> or due to ap do
- allResolvers ← threat.getResolvers(newPlan)
- if allResolvers.empty() then return failuer
- resolver ← allResolvers.chooseOne()
- newPlan ← newPlan.refine(resolver)
- retun Pop(newPlan,agenda)
部分函数的说明 plan.getProviders(pg)
- 确定性的选择点,不需要回溯
- 选出所有可以解决命题pg的行动
relevant.chooseOne()
- 不确定性选择点,可以回溯
- 返回 一个行动ap,该行动的和子目标的命题相关的效果pp,σ是使得未实现子目标和效果一致的某种置换,如,r1 = robot,l1 = loc1
State-Space vs. Plan-Space Planning

总结: 状态空间的节点由有限的状态组成,这些状态是各种已知的世界状态。使用状态空间进行规划,需要准备好规划问题的定义域,即 ∑ = (S,A,γ)
- S为所有状态点集
- A为所有行动的集合
- γ为过渡系统,其定义了所有状态的过渡映射
- 即,s’ = γ(s,a), 在s状态,应用动作a,可以得到状态s’
然后准备搜索问题,P = (O,si,g)
- 初始状态:si
- 最终目标的满足检测: 如果当前s 满足 g时,说明找到终点
- 路径成本函数:
π = |π|,等于路径的长度 - 状态s后继节点函数 : Γ(s)
接下来就可以进行路径(解决方案)搜索了。搜索期间使用到的启发式这些就不再多说,就是优化挑选成本,选择最短的路径,成本最低的路径。
最后我们讲到因为这种在状态空间中搜索的缺点,就是在一些极端情况下,有非常耗时,不必要的搜索,不管是使用哪种启发式,前面得到一些肯定没有抵达终点路径的节点,但是在意识到之前已经遍历完毕,所以说浪费时间。 因此,我们才提出了PSP算法,在状态空间中进行的局部规划,大大减少了搜索空间,接而进一步改进PSP得到PoP算法。


